
����Ŀ����ͼ����E�Ǿ���ABCD�ĶԽ���BD�ϵ�һ�㣬��BE=BC��AB=3��BC=4����PΪֱ��EC�ϵ�һ�㣬��PQ��BC�ڵ�Q��PR��BD�ڵ�R�� 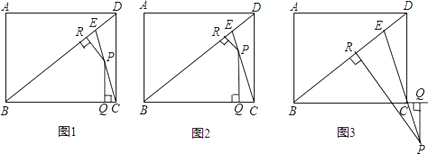
��1������ͼ1������PΪ�߶�EC�е�ʱ����֤��PR+PQ= ![]() ������֤������ ����ͼ2������PΪ�߶�EC�ϵ�����һ�㣨�����E����C�غϣ�ʱ�������������䣬����еĽ����Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
������֤������ ����ͼ2������PΪ�߶�EC�ϵ�����һ�㣨�����E����C�غϣ�ʱ�������������䣬����еĽ����Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
��2����ͼ3������PΪ�߶�EC�ӳ����ϵ�����һ��ʱ�������������䣬��PR��PQ֮���־���������������ϵ����ֱ��д����IJ��룮
���𰸡�
��1���⣺ͼ2�н���PR+PQ= ![]() �Գ�����
�Գ�����
֤��������BP����C����CK��BD�ڵ�K��
���ı���ABCDΪ���Σ�
���BCD=90�㣬
�֡�CD=AB=3��BC=4��
��BD= ![]() =5��
=5��
��S��BCD= ![]() BCCD=
BCCD= ![]() BDCK��
BDCK��
��3��4=5CK��
��CK= ![]() ��
��
��S��BCE= ![]() BECK��S��BEP=
BECK��S��BEP= ![]() PRBE��
PRBE��
S��BCP= ![]() PQBC����S��BCE=S��BEP+S��BCP��
PQBC����S��BCE=S��BEP+S��BCP��
�� ![]() BECK=
BECK= ![]() PRBE+
PRBE+ ![]() PQBC��
PQBC��
�֡�BE=BC��
�� ![]() CK=
CK= ![]() PR+
PR+ ![]() PQ��
PQ��
��CK=PR+PQ��
�֡�CK= ![]() ��
��
��PR+PQ= ![]() ��
��

��2���⣺��C��CF��BD��BD��F����CM��PR��PR��M������BP��
S��BPE��S��BCP=S��BEC��S��BEC�ǹ̶�ֵ��
BE=BCΪ�����ף�PR��PQ �ֱ�Ϊ�ߣ�ͼ3�еĽ�����PR��PQ= ![]()
����������1��������BP����C����CK��BD�ڵ�K�����ݾ��ε����ʼ����ɶ������BD�ij������������������ȿ����CK�ij������ͨ��������������֤������2��ͼ3�еĽ�����PR��PQ= ![]() ��
��
�����㾫����������Ҫ�����������ε�������ɶ����ĸ�������֪ʶ�㣬��Ҫ���������ε����=1/2���ס��ߣ�ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2������ȷ�����⣮


 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ���������֣�Ȼ�������⣮
���֪��![]() ������������������������ѭ��С�������
������������������������ѭ��С�������![]() ��С���������Dz�����ȫ��д����������С����
��С���������Dz�����ȫ��д����������С����![]() ��1��ʾ
��1��ʾ![]() ��С�����֣���ͬ��С���ı�ʾ��������ʵ�ϣ�С���ı�ʾ�������е����ģ���Ϊ
��С�����֣���ͬ��С���ı�ʾ��������ʵ�ϣ�С���ı�ʾ�������е����ģ���Ϊ![]() ������������1�����������ȥ���������֣������С�����֣�
������������1�����������ȥ���������֣������С�����֣�
�ɴ����ǻ����Եõ�һ�������⣺���![]() =x+y������x����������0��y��1����ôx=1��y=
=x+y������x����������0��y��1����ôx=1��y=![]() ��1��
��1��
�����������⣺
��1�����![]() =a+b������a����������0��b��1����ôa=�� ����b=�� ����
=a+b������a����������0��b��1����ôa=�� ����b=�� ����
��2����֪2+![]() =m+n������m����������0��n��1����|m��n|��ֵ��
=m+n������m����������0��n��1����|m��n|��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAC=��DAF=90����AB=AC��AD=AF����D��EΪBC���ϵ����㣬����DAE=45��������EF��BF�������н��ۣ��١�AED�ա�AEF ����ABE�ס�ACD����BE��DC��DE��BE2��DC2=DE2��������ȷ������ ����
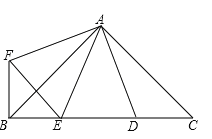
A��1 B��2 C��3 D��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������δ֪������������̣�������⣩�����������̶ӣ�������30�����Ҷ�����10�����������������ӵ�����������ʹ�ӵ��������Ҷ�������7����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AD��BC������ΪD����B=60�㣬��C=45�㣮 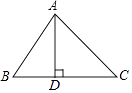
��1�����BAC�Ķ�����
��2����AC=2����AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�ڲ������ɸ��㣬����Щ���Լ�������ABCD�Ķ���A��B��C��D��ԭ�����ηָ��һЩ������������ص�����

��1��������
������ABCD�ڵ�ĸ��� | 1 | 2 | 3 | 4 | �� | n |
�ָ�ɵ������εĸ��� | 4 | 6 | �� |
��2��ԭ�������ָܷ��2016�������Σ����ܣ����ʱ������ABCD�ڲ��ж��ٸ��㣿�����ܣ���˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽��У�������ί������40��ѧУ���꼶ѧ�����������ҵʱ����к������ͳ�ƣ��������ռ������ݻ���������������������ͳ��ͼ���������ͼ���ṩ����Ϣ�������������⣺
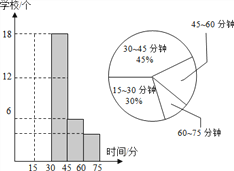
(1)�����ѧ�����������ҵʱ����3045���ӵ�ѧУ��Ӧ������Բ�Ľǣ�
(2)��ͼ�е�����ͼ����������
(3)�����ѧ�����������ҵʱ����6075���ӵ�ѧУռ����ѧУ�����İٷֱȡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�E��BC���е㣬����ABE��AE�۵���õ���AFE����F�ھ���ABCD�ڲ����ӳ�AF��CD�ڵ�G�� 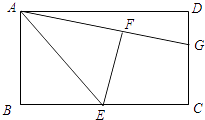
��1�������߶�GF��GC�к�������ϵ����֤����Ľ��ۣ�
��2����AB=3��AD=4�����߶�GC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ�ҳ̴�λ�ġ��㷨ͳ�ڡ���������һ�����⣨��ͼ���������Ϊ����һȺ�˷����ӣ����ÿ�˷���������ʣ�����������ÿ�˷־���������������ʣ����ֵ����ӹ���������ע������ʱ1��=16�������С���������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com