
【题目】先阅读下面的文字,然后解答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,于是小明用
的小数部分我们不可能全部写出来,于是小明用![]() ﹣1表示
﹣1表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
由此我们还可以得到一个真命题:如果![]() =x+y,其中x是整数,且0<y<1,那么x=1,y=
=x+y,其中x是整数,且0<y<1,那么x=1,y=![]() ﹣1.
﹣1.
请解答下列问题:
(1)如果![]() =a+b,其中a是整数,且0<b<1,那么a= ,b= ;
=a+b,其中a是整数,且0<b<1,那么a= ,b= ;
(2)已知2+![]() =m+n,其中m是整数,且0<n<1,求|m﹣n|的值.
=m+n,其中m是整数,且0<n<1,求|m﹣n|的值.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
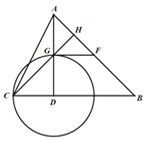
【题目】如图,在△ABC中,∠B=45°,AD⊥BC于点D,以D为圆心DC为半径作⊙D交AD于点G,过点G作⊙D的切线交AB于点F,且F恰好为AB中点.
(1)求tan∠ACD的值.
(2)连结CG并延长交AB于点H,若AH=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】调查收集数据时,一般要设计调查问卷.设计的调查问卷中应包括( )
A.调查的问题和调查的对象
B.调查的目的和调查的内容
C.调查的方法
D.以上内容都应具备
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司承接A、B两种货物运输业务,已知5月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;6月份由于油价上涨,运费单价上涨为:A货物70元/吨,B货物40元/吨;该物流公司6月承接的A种货物和B种数量与5月份相同,6月份共收取运费13000元.
(1)该物流公司月运输两种货物各多少吨?
(2)该物流公司预计7月份运输这两种货物330吨,且A货物的数量不大于B货物的2倍,在运费单价与6月份相同的情况下,该物流公司7月份最多将收到多少运输费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以原点O为位似中心,作△ABC的位似图形△A'B'C',△ABC与△A'B'C'相似比为1:3,若点C的坐标为(4,1),则点C’的坐标为( )
A.(12,3)B.(﹣12,3)或(12,﹣3)
C.(﹣12,﹣3)D.(12,3)或(﹣12,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD的对角线BD上的一点,且BE=BC,AB=3,BC=4,点P为直线EC上的一点,且PQ⊥BC于点Q,PR⊥BD于点R. 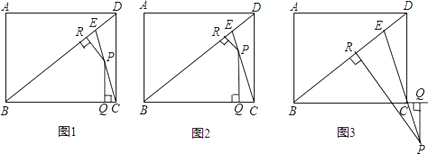
(1)①如图1,当点P为线段EC中点时,易证:PR+PQ= ![]() (不需证明). ②如图2,当点P为线段EC上的任意一点(不与点E、点C重合)时,其它条件不变,则①中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
(不需证明). ②如图2,当点P为线段EC上的任意一点(不与点E、点C重合)时,其它条件不变,则①中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
(2)如图3,当点P为线段EC延长线上的任意一点时,其它条件不变,则PR与PQ之间又具有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com