
【题目】如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论:①∠AED=∠ADC;②![]() ;③AC
;③AC![]() BE=12;④3BF=4AC;其中正确结论的个数有( )
BE=12;④3BF=4AC;其中正确结论的个数有( )
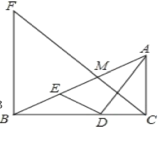
A.1个B.2个C.3个D.4个
【答案】C
【解析】
选项①∠AED=90°-∠EAD,∠ADC=90°-∠DAC,∠EAD=∠DAC;
②易证△ADE∽△ACD,得DE:DA=DC:AC=3:AC,AC不一定等于6;
③根据相似三角形的判定定理得出△BED∽△BDA,再由相似三角形的对应边成比例即可得出结论;
④连接DM,可证DM∥BF∥AC,得FM:MC=BD:DC=4:3;易证△FMB∽△CMA,得比例线段求解.
∠AED=90°∠EAD,∠ADC=90°∠DAC,

∵AD平分∠BAC
∴∠EAD=∠DAC,
∴∠AED=∠ADC.
故①选项正确;
∵∠EAD=∠DAC,∠ADE=∠ACD=90°,
∴△ADE∽△ACD,得DE:DA=DC:AC=3:AC,但AC的值未知,
故②不一定正确;
由①知∠AED=∠ADC,
∴∠BED=∠BDA,
又∵∠DBE=∠ABD,
∴△BED∽△BDA,
∴DE:DA=BE:BD,由②知DE:DA=DC:AC,
∴BE:BD=DC:AC,
∴ACBE=BDDC=12.
故③选项正确;
连接DM,则DM=MA.
∴∠MDA=∠MAD=∠DAC,
∴DM∥BF∥AC,
由DM∥BF得FM:MC=BD:DC=4:3;
由BF∥AC得△FMB∽△CMA,有BF:AC=FM:MC=4:3,
∴3BF=4AC.
故④选项正确.
综上所述,①③④正确,共有3个.
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在4×4的正方形网格中,△ABC和△A'B'C'的顶点都在边长为1的小正方形的格点上.

(1)填空:∠BAC= °,AB= ;
(2)判断:△ABC和△A'B'C这两个三角形相似吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》、《大学》、《中庸》(依次用字母A,B,C表示这三个材料),将A,B,C分别写在3张完全相同的不透明卡片的正面上,背面朝上洗匀后放在桌面上,比赛时小礼先从中随机抽取一张卡片,记下内容后放回,洗匀后,再由小智从中随机抽取一张卡片,他俩按各自抽取的内容进行诵读比赛.
(1)小礼诵读《论语》的概率是 ;(直接写出答案)
(2)请用列表或画树状图的方法求他俩诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G.连接EF,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.则正确结论的序号是( )
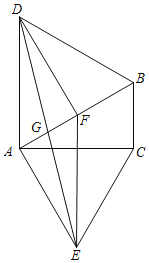
A.①③B.②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD//BC,AB=DC,过点D作DE⊥BC,垂足为E,并延长DE至F,使EF=DE.联结BF、CD、AC.
(1)求证:四边形ABFC是平行四边形;
(2)如果DE2=BE·CE,求证四边形ABFC是矩形.
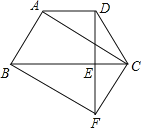
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象交x轴于点A,B(点A在点B的左侧).
的图象交x轴于点A,B(点A在点B的左侧).
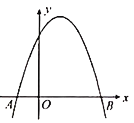
(1)求点A,B的坐标,并根据该函数图象写出y≥0时x的取值范围;
(2)把点B向上平移m个单位得点B1.若点B1向左平移n个单位,将与该二次函数图象上的点B2重合;若点B1向左平移(n+6)个单位,将与该二次函数图象上的点B3重合.已知m>0,n>0,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自1993年起,联合国将每年的3月22日定为“世界水日”,宗旨是唤起公众的节水意识,加强水资源保护.某校在开展“节约每一滴水”的活动中,从初三年级随机选出20名学生统计出各自家庭一个月的节约用水量,有关数据整理如下表.
节约用水量(单位:吨) | 1 | 1.2 | 1.4 | 2 | 2.5 |
家庭数 | 4 | 6 | 5 | 3 | 2 |
这组数据的中位数和众数分别是( )
A. 1.2,1.2; B. 1.4,1.2; C. 1.3,1.4; D. 1.3,1.2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com