
【题目】如图,在4×4的正方形网格中,△ABC和△A'B'C'的顶点都在边长为1的小正方形的格点上.

(1)填空:∠BAC= °,AB= ;
(2)判断:△ABC和△A'B'C这两个三角形相似吗?为什么?
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:
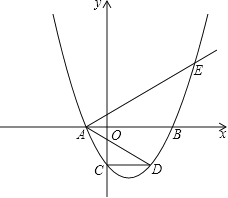
【题目】如图,二次函数![]() (其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(1)用含m的代数式表示a;
(2))求证:![]() 为定值;
为定值;
(3)设该二次函数图象的顶点为F.探索:在x轴的负半轴上是否存在点G,连接CF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.
(1)求∠AFE的度数;
(3)求阴影部分的面积(结果保留π和根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一边长为l的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OBl为边作第三个正方形OBlB2C2,照此规律作下去,则点B2020的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场举办抽奖活动,规则如下:在不透明的袋子中有2个红球和2个黑球,这些球除颜色外都相同,顾客每次摸出一个球,若摸到红球,则获得1份奖品,若摸到黑球,则没有奖品。
(1)如果小芳只有一次摸球机会,那么小芳获得奖品的概率为 ;
(2)如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率。(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A为x轴上一点,以OA为直径的作半圆M,点B为OA上一点,以OB为边作□OBDC交半圆M于C,D两点.
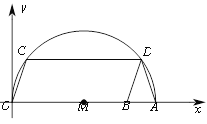
(1)连接AD,求证:DA=DB;
(2)若A点坐标为(20,0),点B的坐标是(16,0),求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
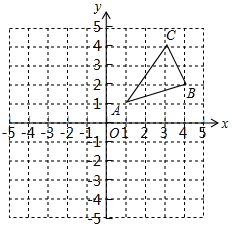
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)请直接判断四边形CBC2B2的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
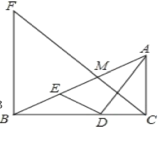
【题目】如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论:①∠AED=∠ADC;②![]() ;③AC
;③AC![]() BE=12;④3BF=4AC;其中正确结论的个数有( )
BE=12;④3BF=4AC;其中正确结论的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com