
【题目】在半径为2的⊙O中,弦AB=![]() ,连接OA,OB.在直线OB上取一点K,使tan∠BAK=
,连接OA,OB.在直线OB上取一点K,使tan∠BAK=![]() ,则ΔOAK的面积为___________.
,则ΔOAK的面积为___________.
【答案】![]() 或6
或6
【解析】
根据题意,建立直角三角形,根据锐角三角函数值求得OK的长度,从而求得三角形面积.
解:
情况一:如图,过点K作KM⊥AB
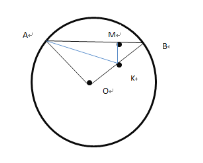
由题意可知,OA=OB=2,AB=![]()
∵![]()
∴△AOB为等腰直角三角形
∴∠OAB=∠OBA=45°
∵tan∠BAK=![]()
∴在Rt△AKM中,![]()
设MK=x,则AM=2x,MB=x,则AB=3x
∴3x=![]()
解得:x=![]()
∴MK=MB=![]() ,BK=
,BK=![]()
∴OK=OB-BK=![]()
∴S△AOK=![]()
情况二:如图,过点K作KM⊥AB
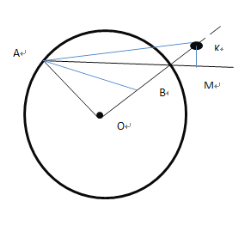
由题意可知,OA=OB=2,AB=![]()
∵![]()
∴△AOB为等腰直角三角形
∴∠OAB=∠OBA=45°
∵tan∠BAK=![]()
∴在Rt△AKM中,![]()
设MK=x,则AM=2x,MB=x,则AB=x
∴x=![]()
∴BK=![]()
∴OK=OB-BK=![]()
∴S△AOK=![]()
综上所述,故答案为:![]() 或6
或6


科目:初中数学 来源: 题型:
【题目】已知二次函数的图象与x轴交于A(-2,0)、B(3,0)两点,且函数有最大值是2.
(1)求二次函数的图象的解析式;
(2)设此二次函数的顶点为P,求△ABP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在4×4的正方形网格中,△ABC和△A'B'C'的顶点都在边长为1的小正方形的格点上.

(1)填空:∠BAC= °,AB= ;
(2)判断:△ABC和△A'B'C这两个三角形相似吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为( )

A.16 B.15 C.14 D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,
中点,![]() 是
是![]() 的外角
的外角![]() 的角平分线,延长
的角平分线,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
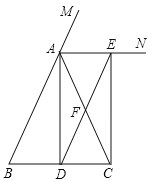
(1)求证:四边形![]() 是矩形;
是矩形;
(2)填空:
①若![]() ,则四边形
,则四边形![]() 的面积为_______;
的面积为_______;
②当![]() 满足______时,四边形
满足______时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
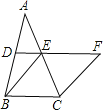
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》、《大学》、《中庸》(依次用字母A,B,C表示这三个材料),将A,B,C分别写在3张完全相同的不透明卡片的正面上,背面朝上洗匀后放在桌面上,比赛时小礼先从中随机抽取一张卡片,记下内容后放回,洗匀后,再由小智从中随机抽取一张卡片,他俩按各自抽取的内容进行诵读比赛.
(1)小礼诵读《论语》的概率是 ;(直接写出答案)
(2)请用列表或画树状图的方法求他俩诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G.连接EF,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.则正确结论的序号是( )
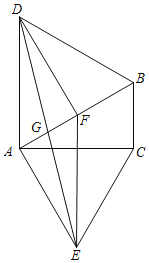
A.①③B.②④C.①③④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com