
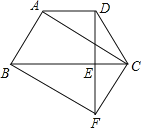
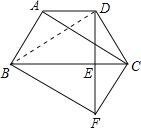
【题目】如图,在梯形ABCD中,AD//BC,AB=DC,过点D作DE⊥BC,垂足为E,并延长DE至F,使EF=DE.联结BF、CD、AC.
(1)求证:四边形ABFC是平行四边形;
(2)如果DE2=BE·CE,求证四边形ABFC是矩形.
【答案】 (1) 证明见解析;(2) 证明见解析.
【解析】
(1)连接BD,利用等腰梯形的性质得到AC=BD,再根据垂直平分线的性质得到DB=FB,从而得到AC=BF,然后证得AC∥BF,利用一组对边平行且相等判定平行四边形;(2)利用题目提供的等积式和两直角相等可以证得两直角三角形相似,得到对应角相等,从而得到直角来证明有一个角是直角的平行四边形是矩形.
(1)连接BD,
∵梯形ABCD中,AD∥BC,AB=CD,
∴AC=BD,
∵DE⊥BC,EF=DE,
∴BD=BF,CD=CF,
∴AC=BF,AB=CF,
∴四边形ABFC是平行四边形;
(2)∵DE2=BECE
∴![]() ,
,
∵∠DEB=∠DEC=90°,
∴△BDE∽△DCE,
∴∠CDE=∠DBE,
∴∠BFC=∠BDC=∠BDE+∠CDE=∠BDE+∠DBE=90°,
∴四边形ABFC是矩形.


科目:初中数学 来源: 题型:
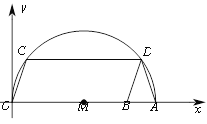
【题目】如图,在平面直角坐标系xOy中,A为x轴上一点,以OA为直径的作半圆M,点B为OA上一点,以OB为边作□OBDC交半圆M于C,D两点.
(1)连接AD,求证:DA=DB;
(2)若A点坐标为(20,0),点B的坐标是(16,0),求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
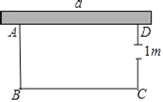
【题目】如图,有一农户要建一个矩形鸡舍,鸡舍的一边利用长为a米的墙,另外三边用25米长的篱笆围成,为方便进出,在垂直于墙的一边CD上留一个1米宽的门,
(1)若a=12,问矩形的边长分别为多少时,鸡舍面积为80米2.
(2)问a的值在什么范围时,(1)中的解有两个?一个?无解?
(3)若住房墙的长度足够长,问鸡舍面积能否达到90平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好数学的甲、乙两个同学做了一个数字游戏:拿出三张正面写有数字﹣1,0,1且背面完全相同的卡片,将这三张卡片背面朝上洗匀后,甲先随机抽取一张,将所得数字作为p的值,然后将卡片放回并洗匀,乙再从这三张卡片中随机抽取一张,将所得数字作为q值,两次结果记为![]() .
.
(1)请你帮他们用树状图或列表法表示![]() 所有可能出现的结果;
所有可能出现的结果;
(2)求满足关于x的方程![]() 没有实数根的概率.
没有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论:①∠AED=∠ADC;②![]() ;③AC
;③AC![]() BE=12;④3BF=4AC;其中正确结论的个数有( )
BE=12;④3BF=4AC;其中正确结论的个数有( )
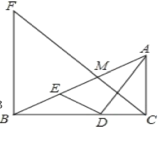
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式为“单人组”和“双人组”.小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华商场为迎接家电下乡活动销售某种冰箱,每台进价为2500元,市场调研表明;当销售价定为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
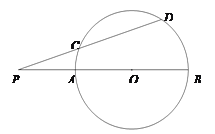
【题目】已知P是![]() 的直径BA延长线上的一个动点,∠P的另一边交
的直径BA延长线上的一个动点,∠P的另一边交![]() 于点C、D,两点位于AB的上方,
于点C、D,两点位于AB的上方,![]() =6,OP=m,
=6,OP=m,![]() ,如图所示.另一个半径为6的
,如图所示.另一个半径为6的![]() 经过点C、D,圆心距
经过点C、D,圆心距![]() .
.
(1)当m=6时,求线段CD的长;
(2)设圆心O1在直线![]() 上方,试用n的代数式表示m;
上方,试用n的代数式表示m;
(3)△POO1在点P的运动过程中,是否能成为以OO1为腰的等腰三角形,如果能,试求出此时n的值;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com