
【题目】在证明“勾股定理”时,可以将4个全等的直角三角形和一个小正方形拼成的一个大正方形(如图所示).如果小正方形的面积是25,大正方形的面积为49,直角三角形中较小的锐角为α,那么tanα的值是____.

科目:初中数学 来源: 题型:
【题目】2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两个探测点探测到C处是信号发射点,已知A、B两点相距400m,探测线与海平面的夹角分别是![]() 和
和![]() ,若CD的长是点C到海平面的最短距离.
,若CD的长是点C到海平面的最短距离.
![]() 问BD与AB有什么数量关系,试说明理由;
问BD与AB有什么数量关系,试说明理由;
![]() 求信号发射点的深度
求信号发射点的深度![]() 结果精确到1m,参考数据:
结果精确到1m,参考数据:![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )

A.AQ= PQ B.AQ=3PQ C.AQ=![]() PQ D.AQ=4PQ
PQ D.AQ=4PQ
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为F.
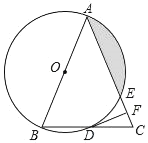
(1)求证:DF为⊙O的切线;
(2)若![]() ,∠CDF=22.5°,求阴影部分的面积.
,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
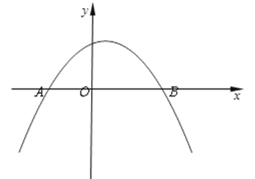
【题目】如图,已知平面直角坐标系![]() ,抛物线
,抛物线![]() 与
与![]() 轴交于点A(-2,0)和点B(4,0) .
轴交于点A(-2,0)和点B(4,0) .
(1)求这条抛物线的表达式和对称轴;
(2)点C在线段OB上,过点C作CD⊥![]() 轴,垂足为点C,交抛物线与点D,E是BD中点,联结CE并延长,与
轴,垂足为点C,交抛物线与点D,E是BD中点,联结CE并延长,与![]() 轴交于点F.
轴交于点F.
①当D恰好是抛物线的顶点时,求点F的坐标;
②联结BF,当△DBC的面积是△BCF面积的![]() 时,求点C的坐标.
时,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明研究一函数的性质,下表是该函数的几组对应值:

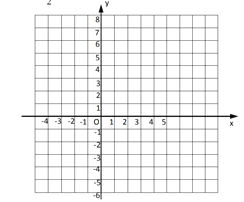
![]() 在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图像
在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图像
![]() 根据所画函数图像,写出该函数的一条性质: .
根据所画函数图像,写出该函数的一条性质: .
![]() 根据图像直接写出该函数的解析式及自变量的取值范围: ;
根据图像直接写出该函数的解析式及自变量的取值范围: ;
![]() 若一次函数
若一次函数![]() 与该函数图像有三个交点,则
与该函数图像有三个交点,则![]() 的范围是 .
的范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标为
的坐标为![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴以每秒
轴以每秒![]() 个单位的速度向上移动,且过点
个单位的速度向上移动,且过点![]() 的直线
的直线![]() 也随之移动,如果点
也随之移动,如果点![]() 关于
关于![]() 的对称点落在坐标轴上,没点
的对称点落在坐标轴上,没点![]() 的移动时间为
的移动时间为![]() ,那么
,那么![]() 的值可以是___.
的值可以是___.
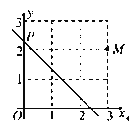
查看答案和解析>>
科目:初中数学 来源: 题型:
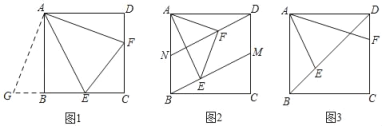
【题目】已知:正方形ABCD,∠EAF=45°.
(1)如图,当点E、F分别在边BC、CD上,连接EF,求证:EF=BE+DF;
童威同学是这样思考的,请你和他一起完成如下解答:证明:将△ADF绕点A顺时针旋转90°,得△ABG,所以△ADF≌△ABG.
(2)如图,点M、N分别在边AB、CD上,且BN=DM.当点E、F分别在BM、DN上,连接EF,探究三条线段EF、BE、DF之间满足的数量关系,并证明你的结论.
(3)如图,当点E、F分别在对角线BD、边CD上.若FC=2,则BE的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com