
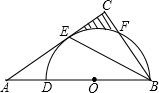
 如图,△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
如图,△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F. 解:(1)连接OE.
解:(1)连接OE.| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 60π×42 |
| 360 |
| 8 |
| 3 |
| 3 |
| 8 |
| 3 |


科目:初中数学 来源: 题型:
 住在郑东新区的小明知道“中原第一高楼”有多高,他登上了附近的另一座高层酒店的顶层某处.已知小明所处位置距离地面有160米高,测得“中原第一高楼”顶部的仰角为37°,测得“中原第一高楼”底部的俯角为45°,请你用初中数学知识帮小明解决这个问题.(请你画出示意图,并说明理由)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
住在郑东新区的小明知道“中原第一高楼”有多高,他登上了附近的另一座高层酒店的顶层某处.已知小明所处位置距离地面有160米高,测得“中原第一高楼”顶部的仰角为37°,测得“中原第一高楼”底部的俯角为45°,请你用初中数学知识帮小明解决这个问题.(请你画出示意图,并说明理由)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:
| A、抛一枚硬币正面朝上的机会与抛一枚图钉钉尖着地的机会一样大 |
| B、为了解汉口火车站某一天中通过的列车车辆数,可采用全面调查的方式进行 |
| C、彩票中奖的机会是1%,买100张一定会中奖 |
| D、中学生小亮,对他所在的那栋住宅楼的家庭进行调查,发现拥有空调的家庭占100%,于是他得出全市拥有空调家庭的百分比为100%的结论 |
查看答案和解析>>
科目:初中数学 来源: 题型:
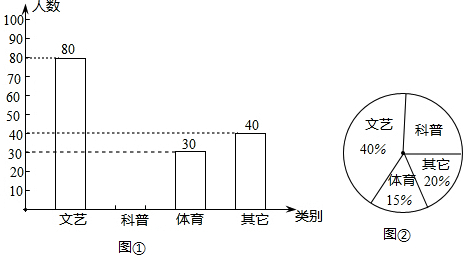
查看答案和解析>>
科目:初中数学 来源: 题型:
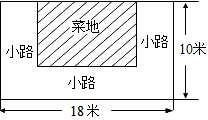 如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其余三面留出宽都是x米小路,中间余下长方形部分做菜地.
如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其余三面留出宽都是x米小路,中间余下长方形部分做菜地.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com