Question

【题目】（1）问题发现．

如图1，和均为等边三角形，点、、均在同一直线上，连接．

①求证：．

②求的度数．

③线段、之间的数量关系为__________．

（2）拓展探究．

如图2，和均为等腰直角三角形，，点、、在同一直线上，为中边上的高，连接．

①请判断的度数为____________．

②线段、、之间的数量关系为________．（直接写出结论，不需证明）

Answer 1

【答案】（1）①详见解析；②60°；③；（2）①90°；②

【解析】

（1）易证∠ACD＝∠BCE，即可求证△ACD≌△BCE，根据全等三角形对应边相等可求得AD＝BE，根据全等三角形对应角相等即可求得∠AEB的大小；

（2）易证△ACD≌△BCE，可得∠ADC＝∠BEC，进而可以求得∠AEB＝90°，即可求得DM＝ME＝CM，即可解题．

解：（1）①证明：∵和均为等边三角形，

∴，，

又∵，

∴，

∴．

②∵为等边三角形，

∴．

∵点、、在同一直线上，

∴，

又∵，

∴，

∴．

③

，

∴．

故填：；

（2）①∵和均为等腰直角三角形，

∴，，

又∵，

∴，

∴，

在和中，

，

∴，

∴．

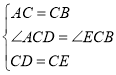∵点、、在同一直线上，

∴，

∴．

②∵，

∴．

∵，，

∴．

又∵，

∴，

∴．

故填：①90°；②．