
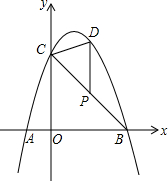
 抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).
抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).分析 (1)由y=-x2+bx+c经过点A、B、C,A(-1,0),C(0,3),利用待定系数法即可求得此抛物线的解析式;
(2)首先令-x2+2x+3=0,求得点B的坐标,然后设直线BC的解析式为y=kx+b′,由待定系数法即可求得直线BC的解析式;
(3)设P(a,3-a),即可得D(a,-a2+2a+3),即可求得PD的长,由S△BDC=S△PDC+S△PDB,即可得S△BDC=-$\frac{3}{2}$(a-$\frac{3}{2}$)2+$\frac{27}{8}$,利用二次函数的性质,即可求得当△BDC的面积最大值.
解答 解:(1)由题意得:$\left\{\begin{array}{l}{-1-b+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
∴抛物线解析式为y=-x2+2x+3;
(2)令-x2+2x+3=0,
解得x1=-1,x2=3,
即B(3,0),
设直线BC的解析式为y=kx+b′,
则$\left\{\begin{array}{l}{b′=3}\\{3k+b′=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b′=3}\end{array}\right.$,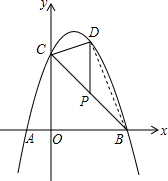
故直线BC的解析式为y=-x+3;
(3)如图,连接BD,
设P(a,3-a),则D(a,-a2+2a+3),
∴PD=(-a2+2a+3)-(3-a)=-a2+3a,
∴S△BDC=S△PDC+S△PDB
=$\frac{1}{2}$PD•a+$\frac{1}{2}$PD•(3-a)
=$\frac{1}{2}$PD×3
=$\frac{3}{2}$(-a2+3a)
=-$\frac{3}{2}$(a-$\frac{3}{2}$)2+$\frac{27}{8}$,
∴当a=$\frac{3}{2}$时,△BDC的面积最大为$\frac{27}{8}$.
点评 此题考查了待定系数法求函数的解析式、二次函数的最值问题以及三角形面积表示方法等知识,根据题意表示出S△BDC=S△PDC+S△PDB是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 晚上,小明有路灯A走向路灯B,当他走到点P时,发现身后身后他的影子的顶部刚好接触路灯A的底部,当他向前再走12米到达Q时,发现身前他的影子的顶部刚好接触到路灯B的底部.已知,小明身高1.6米,两路灯的高AC=BD=9.6米,
晚上,小明有路灯A走向路灯B,当他走到点P时,发现身后身后他的影子的顶部刚好接触路灯A的底部,当他向前再走12米到达Q时,发现身前他的影子的顶部刚好接触到路灯B的底部.已知,小明身高1.6米,两路灯的高AC=BD=9.6米,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
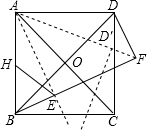 如图,在正方形ABCD中,AB=4,将△ADC绕点A顺时针旋转α(0<α<45°),记旋转后的三角形为△AD′C′,过点B作BE⊥AC′于点E,延长BE交射线AD′于点F,连接DF,取AB中点H,连接HE,在旋转过程中,当HE⊥BD时,(BE+DF)2的值为8+4$\sqrt{2}$.
如图,在正方形ABCD中,AB=4,将△ADC绕点A顺时针旋转α(0<α<45°),记旋转后的三角形为△AD′C′,过点B作BE⊥AC′于点E,延长BE交射线AD′于点F,连接DF,取AB中点H,连接HE,在旋转过程中,当HE⊥BD时,(BE+DF)2的值为8+4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图梯形ABCD中,AD∥BC,O为对角线的交点,F为OB上一点,E为CF上一点,S△AOB=10,S△BFE=3,S△BEC=9,S△OEC=6,试求梯形ABCD的面积.
如图梯形ABCD中,AD∥BC,O为对角线的交点,F为OB上一点,E为CF上一点,S△AOB=10,S△BFE=3,S△BEC=9,S△OEC=6,试求梯形ABCD的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com