
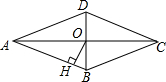
 如图,菱形ABCD的对角线AC、BD相交于点O,∠ADC=135°,过点O作OH⊥AB,垂足为H,则∠AOH=67.5度.
如图,菱形ABCD的对角线AC、BD相交于点O,∠ADC=135°,过点O作OH⊥AB,垂足为H,则∠AOH=67.5度. 分析 先根据菱形的性质得到∠ABD=$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ADC=67.5°,BD⊥AC,则∠OAB+∠ABO=90°,加上∠OAB+∠AOH=90°,则利用等角的余角相等即可得到∠AOH的度数.
解答 解:∵四边形ABCD为菱形,
∴∠ABD=$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ADC=$\frac{1}{2}$×135°=67.5°,BD⊥AC,
∴∠OAB+∠ABO=90°,
∵OH⊥AB,
∴∠OAB+∠AOH=90°,
∴∠AOH=∠ABD=67.5°.
故答案为67.5.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
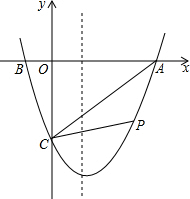 已知(如图所示):抛物线y=ax2+bx+c经过点A(3,0)、C(0,-3)其对称轴为x=1.
已知(如图所示):抛物线y=ax2+bx+c经过点A(3,0)、C(0,-3)其对称轴为x=1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
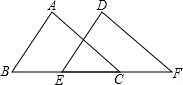 如图,在△ABC和△DEF中,∠A=∠D,AC=DF,若根据“ASA”说明△ABC≌△DEF,则应添加条件∠ACB=DFE.或AC∥DF.
如图,在△ABC和△DEF中,∠A=∠D,AC=DF,若根据“ASA”说明△ABC≌△DEF,则应添加条件∠ACB=DFE.或AC∥DF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
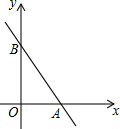 如图,直线y=kx+b交坐标轴于A(3,0)、B(0,5)两点,则不等式kx+b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(3,0)、B(0,5)两点,则不等式kx+b<0的解集为( )| A. | x<3 | B. | x>3 | C. | x<5 | D. | x>5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
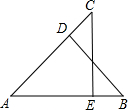 如图,△ABD≌△ACE,且∠BAD和∠CAE,∠ABD和∠ACE,∠ADB和∠AEC是对应角,则对应边AB与AC,AD与AE,BD与CE.
如图,△ABD≌△ACE,且∠BAD和∠CAE,∠ABD和∠ACE,∠ADB和∠AEC是对应角,则对应边AB与AC,AD与AE,BD与CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
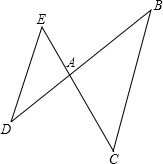 如图,在三角形ABC中,D是BA延长线上一点,E是CA延长线上一点,∠B=31°,∠D=31°,∠E=69°.
如图,在三角形ABC中,D是BA延长线上一点,E是CA延长线上一点,∠B=31°,∠D=31°,∠E=69°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
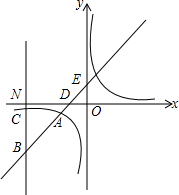 如图,一次函数y=kx+1(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象有公共点A(-2,n),直线l⊥x轴于点N(-5,0),与一次函数和反比例函数的图象分别交于点B、C,一次函数y=kx+1与x轴、y轴分别交于点D、E,且tan∠ADN=1.
如图,一次函数y=kx+1(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象有公共点A(-2,n),直线l⊥x轴于点N(-5,0),与一次函数和反比例函数的图象分别交于点B、C,一次函数y=kx+1与x轴、y轴分别交于点D、E,且tan∠ADN=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com