
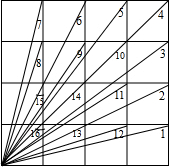
 如图,是一个4×4的方格,
如图,是一个4×4的方格,分析 (1)由图可找出多对全等三角形,根据全等三角形的对应角相等得出对应多对角的和是90°,即∠1+∠7=90°、∠2+∠6=90°、∠3+∠5=90°、∠8+∠12=90°、∠9+∠11=90°、∠13+∠15=90°、且∠4=∠10=∠14=∠16=45°,再相加即可;
(2)首先将原式变形为(∠1+∠3+…+∠15)-(∠2+∠4+…+∠16),再根据对应多对角的和是90°即可求解.
解答 解:(1)观察图形可知:∠1所在的三角形与∠7所在的三角形全等,∠1与∠7的余角相等,也就是∠1与∠7互余,同理:∠2与∠6互余,∠3与∠5互余,∠8与∠12互余,∠9与∠11互余,∠13与∠15互余,又∠4=∠10=∠14=∠16=45°,
∴∠1+∠7=90°、∠2+∠6=90°、∠3+∠5=90°、∠8+∠12=90°、∠9+∠11=90°、∠13+∠15=90°、∠4=∠10=∠14=∠16=45°,
∴∠1+∠2+∠3+…+∠9=90°×6+45°×4=720°.
(2)∠1-∠2+∠3-∠4+…+∠15-∠16
=(∠1+∠3+…+∠15)-(∠2+∠4+…+∠16)
=(∠1+∠7)+(∠3+∠5)+(∠9+∠11)+(∠13+∠15)-(∠2+∠6)-(∠8+∠12)-∠4-∠10-∠14-∠16
=90°×4-90°×2-45°×4
=0.
点评 本题考查三角形全等的性质的运用,由三角形全等得对应角相等.认真观察图形,发现并利用全等三角形是正确解决本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com