
【题目】已知二次函数y=a(x2)2+3的图象经过点(1,0).
(1)求这个二次函数的解析式;
(2)分别指出这个二次函数图象的开口方向、对称轴和顶点坐标.
(3) 写出把此抛物线向右平移1个单位长度,再向上平移2个单位长度后的抛物线解析式。
【答案】(1) 函数解析式为y=![]() (x2)2+3;(2)顶点坐标为(2,3),对称轴为直线x=2;(3)y= -
(x2)2+3;(2)顶点坐标为(2,3),对称轴为直线x=2;(3)y= -![]() (x3)2+5.
(x3)2+5.
【解析】试题分析:(1)将(-1,0)代入二次函数解析式求出a;(2)由函数解析式直接判断开口方向、对称轴和顶点坐标;(3)牢记口诀,上加下减左加右减.
试题解析:
(1)把(1,0)代入二次函数解析式得:9a+3=0,即a=![]() ,
,
则函数解析式为y=![]() (x2)2+3;
(x2)2+3;
(2)∵a=![]() <0,
<0,
∴抛物线开口向下,
顶点坐标为(2,3),对称轴为直线x=2.
(3)抛物线y=![]() (x2)2+3向右平移1个单位长度所得解析式为:y=
(x2)2+3向右平移1个单位长度所得解析式为:y=![]() (x3)2+3,
(x3)2+3,
再向上平移2个单位长度后,所得函数的表达式为:y=![]() (x3)2+3+2=
(x3)2+3+2=![]() (x3)2+5.
(x3)2+5.
故答案为:y= ![]() (x3)2+5.
(x3)2+5.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】在体育课上,对七年级男生进行引体向上测试.以做4个为标准,超过的个数记作正数,不足的个数记作负数其中8名男生做引体向上的个数记录如下:
+3 | -1 | 1 | +3 | 1 | 0 | +2 | -1 |
这8名男生平均每人做了多少个引体向上?
查看答案和解析>>
科目:初中数学 来源: 题型:
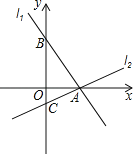
【题目】如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.
(1)求点B的坐标;
(2)若△ABC的面积为4,求直线l2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
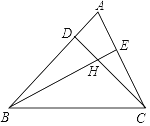
(1)若BE⊥AC,CD⊥AB,求∠BHC的度数.
(2)若BE、CD平分∠ABC和∠ACB,求∠BHC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(-5,0),B(5,0),
(1)写出C点的坐标;
(2)动点P从B点出发以每秒1个单位的速度沿BA方向运动,同时动点Q从C点出发也以每秒1个单位的速度沿y轴正半轴方向运动(当P点运动到A点时,两点都停止运动).设从出发起运动了x秒.
①请用含x的代数式分别表示P,Q两点的坐标;
②当x=2时,y轴上是否存在一点E,使得△AQE的面积与△APQ的面积相等?若存在,求E的坐标,若不存在,说明理由?
(3)在点P、Q运动过程中,过点Q作x轴的平行线DE,∠DQP与∠APQ的角平分线交于点M,则∠PMQ的大小会随点P、Q的运动而变化吗?如果不变化,请求出∠PMQ的度数;若发生变化,请说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
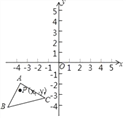
【题目】如图,△A′B′C′是△ABC经过平移得到的,△ABC三个顶点的坐标分别为A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)
(1)请写出三角形ABC平移的过程;
(2)写出点A′,C′的坐标;
(3)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com