
【题目】如图,在平面直角坐标系中,已知点A(-5,0),B(5,0),
(1)写出C点的坐标;
(2)动点P从B点出发以每秒1个单位的速度沿BA方向运动,同时动点Q从C点出发也以每秒1个单位的速度沿y轴正半轴方向运动(当P点运动到A点时,两点都停止运动).设从出发起运动了x秒.
①请用含x的代数式分别表示P,Q两点的坐标;
②当x=2时,y轴上是否存在一点E,使得△AQE的面积与△APQ的面积相等?若存在,求E的坐标,若不存在,说明理由?
(3)在点P、Q运动过程中,过点Q作x轴的平行线DE,∠DQP与∠APQ的角平分线交于点M,则∠PMQ的大小会随点P、Q的运动而变化吗?如果不变化,请求出∠PMQ的度数;若发生变化,请说明理由。


【答案】(1)C(0,5);(2)①P(5-x,0) Q(0,5+x);②Q(0,18.2)或(0,-4.2);(3)不变,理由见解析.
【解析】试题分析:(1)根据y轴上点的坐标特征写出即可;
(2)①点P沿x轴向左运动,用起始位置的横坐标5减去运动的长度x,纵坐标不变;点Q沿y轴向上运动,用起始位置的纵坐标5加上运动的长度x,横坐标不变;②先求出P、Q的坐标和△APQ的面积,分E在y轴的正半轴和E在y轴的负半轴两种情况,根据三角形的面积公式计算即可;
(3)由DE∥AB得 ∠DQP+∠APQ=180,由QM、PM分别是∠DQP与∠APQ的角平分线得 ∠MQP+∠MPQ=90,根据三角形内角和可知 ∠PMQ=90.
解:(1)由图得,C(0,5)
(2)①由题意得,P(5-x,0) Q(0,5+x)
②当x=2时,P(3,0) Q(0,7)
△APQ的面积=28
因为△AQE的高为:5,所以底边 QE=11.2
所以:Q(0,18.2)或(0,-4.2)
(3)不变。 如图,
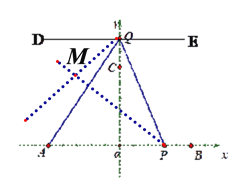
∵DE∥AB,
∴ ∠DQP+∠APQ=180,
∵QM、PM分别是∠DQP与∠APQ的角平分线,
∴ ∠MQP+∠MPQ=90 ,
∴ ∠PMQ=90.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.直线外一点到这条直线的垂线段叫这点到这条直线的距离
B.同位角相等,两直线平行
C.同旁内角一定互补
D.一个角的补角与它的余角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
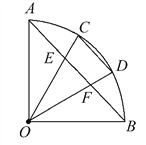
【题目】如图,∠AOB=90°,C,D是![]() 的三等分点,AB分别交OC,OD于点E,F.试找出图中相等的线段(半径除外).
的三等分点,AB分别交OC,OD于点E,F.试找出图中相等的线段(半径除外).
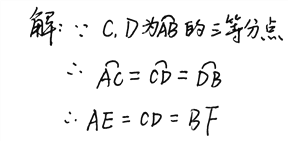
(1)错因: .
(2)纠错:____________________________________________________________
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)方程(x2)216=0的根为______.
(2)解方程:x24x12=0.
(3)解方程:(3y)2+y2=9.
(4)解方程:2x2+6x-5=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x2)2+3的图象经过点(1,0).
(1)求这个二次函数的解析式;
(2)分别指出这个二次函数图象的开口方向、对称轴和顶点坐标.
(3) 写出把此抛物线向右平移1个单位长度,再向上平移2个单位长度后的抛物线解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
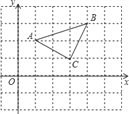
【题目】如图所示,三角形ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).
(1)三角形A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论:①c<3;②当x<-3时,y随x的增大而增大;③若点D的横坐标最大值为5,则点C的横坐标最小值为-5;④当四边形ACDB为平行四边形时, ![]() .其中正确的是( )
.其中正确的是( )
A. ②④ B. ②③ C. ①③④ D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com