
【题目】(1)方程(x2)216=0的根为______.
(2)解方程:x24x12=0.
(3)解方程:(3y)2+y2=9.
(4)解方程:2x2+6x-5=0
【答案】(1)x1=6,x2=2.
(2)x1=6,x2=2.
(3)y1=3,y2=0.
(4)x1=![]() ; x2=
; x2=![]()
【解析】试题分析:(1)首先移项,然后直接开平方解出x即可;(2)将等号左边因式分解成两个因式的积,然后分别令两个因式为0,解出x即可;(3)首先移项,然后将等号左边因式分解成两个因式的积,然后分别令两个因式为0,解出x即可;(4)先将二次项系数化为1,然后移项,配方解出x即可.
试题解析:
(1)移项,得(x2)2=16,
两边直接开平方得:x2=±4,
即x2=4,x2=4,
解得:x1=6,x2=2,
故答案为:x1=6,x2=2.
(2)x24x12=0,
分解因式得:(x6)(x+2)=0,
∴x6=0,x+2=0,
解得:x1=6,x2=2,
故答案为:x1=6,x2=2.
(3)(3y)2+y2=9,
移项,得(3y)2+y2-9=0,
等号左边因式分解,得(y3)2+(y+3)(y-3)=0,(y-3)(y-3+y+3)=0,
即(y-3)2y=0,
∴y-3=0,2y=0,
解得:y1=3,y2=0.
故答案为:y1=3,y2=0.
(4)2x+6x-5=0,
二次项系数化为1,得x+3x-![]() =0,
=0,
移项,得x+3x=![]() ,
,
配方,得x+3x+![]() =
=![]() +
+![]() ,即(x+
,即(x+![]() )=
)=![]() ,
,
解得:x+![]() =
=![]() 或x+
或x+![]() =-
=-![]() ,
,
即x1=![]() ; x2=
; x2=![]() .
.
故答案为:x1=![]() ; x2=
; x2=![]() .
.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣2x+4交y轴于点A,交抛物线![]() 于点B(3,﹣2),抛物线经过点C(﹣1,0),交y轴于点D,点P是抛物线上的动点,作PE⊥DB交DB所在直线于点E.
于点B(3,﹣2),抛物线经过点C(﹣1,0),交y轴于点D,点P是抛物线上的动点,作PE⊥DB交DB所在直线于点E.
(1)求抛物线的解析式;
(2)当△PDE为等腰直角三角形时,求出PE的长及P点坐标;
(3)在(2)的条件下,连接PB,将△PBE沿直线AB翻折,直接写出翻折点后E的对称点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小凡与小光从学校出发到距学校5千米的图书馆看书,小光直接去图书馆, 小凡途中从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:
(1) 是描述小凡的运动过程(填![]() 或
或![]() );
);
(2)小凡和小光先出发的是 ,先出发了 分钟;
(3)小凡与小光先到达图书馆的是 ,先到了 分钟;
(4)求小凡与小光从学校到图书馆的平均速度各是多少?(不包括中间停留的时间)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
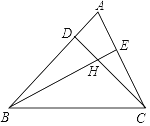
(1)若BE⊥AC,CD⊥AB,求∠BHC的度数.
(2)若BE、CD平分∠ABC和∠ACB,求∠BHC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(-5,0),B(5,0),
(1)写出C点的坐标;
(2)动点P从B点出发以每秒1个单位的速度沿BA方向运动,同时动点Q从C点出发也以每秒1个单位的速度沿y轴正半轴方向运动(当P点运动到A点时,两点都停止运动).设从出发起运动了x秒.
①请用含x的代数式分别表示P,Q两点的坐标;
②当x=2时,y轴上是否存在一点E,使得△AQE的面积与△APQ的面积相等?若存在,求E的坐标,若不存在,说明理由?
(3)在点P、Q运动过程中,过点Q作x轴的平行线DE,∠DQP与∠APQ的角平分线交于点M,则∠PMQ的大小会随点P、Q的运动而变化吗?如果不变化,请求出∠PMQ的度数;若发生变化,请说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,直线y=mx+2与OC,BC两边分别相交于点D,G,以DG为边作菱形DEFG,顶点E在OA边上.
(1)如图1,顶点F在边AB上,当CG=OD时,
求m的值;
菱形DEFG是正方形吗?如果是请给予证明.
(2)如图2,连接BF,设CG=a,△FBG的面积为S,求S与a的函数关系式;
(3)如图3,连接GE,当GD平分∠CGE时,请直接写出m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图,某港口P位于东西方向的海岸线上“远航”号、“海天”号轮船同时离开港口,各自沿同定方向航行,“远航”号每小时航行16n mile,“海天”号每小时航行12n mile,它们离开港口一个半小时后分别位于点Q,R处,且相距30n mile
(1)求PQ,PR的长度;
(2)如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com