Question

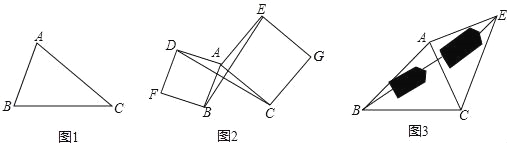
【题目】（1）如图1，已知△ABC，以AB、AC为边向△ABC外作等边△ABD和等边△ACE，连接BE，CD，请你完成图形，并证明：BE=CD；（尺规作图，不写作法，保留作图痕迹）；

（2）如图2，已知△ABC，以AB、AC为边向外作正方形ABFD和正方形ACGE，连接BE，CD，BE与CD有什么数量关系？简单说明理由；

（3）运用（1）、（2）解答中所积累的经验和知识，完成下题：

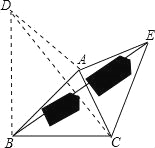
如图3，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，求BE的长．

Answer 1

【答案】（1）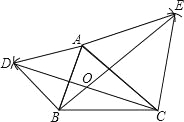

证明见解析；

（2）BE=CD，理由同（1）；

（3）BE=CD=100米．

【解析】

试题分析：（1）分别以A、B为圆心，AB长为半径画弧，两弧交于点D，连接AD，BD，同理连接AE，CE，如图所示，由△ABD与△ACE都是等边三角形，得到三对边相等，两个角相等，都为60度，利用等式的性质得到夹角相等，利用SAS得到△CAD与△EAB全等，利用全等三角形的对应边相等即可得证；

（2）BE=CD，理由与（1）同理；

（3）根据（1）、（2）的经验，过A作等腰直角△ABD，连接CD，由AB=AD=100，利用勾股定理求出BD的长，由题意得到△DBC为直角三角形，利用勾股定理求出CD的长，即为BE的长．

试题解析：（1）完成图形，如图所示：

证明：∵△ABD和△ACE都是等边三角形，

∴AD=AB，AC=AE，∠BAD=∠CAE=60°，

∴∠BAD+∠BAC=∠CAE+∠BAC，即∠CAD=∠EAB，

∵在△CAD和△EAB中，

，

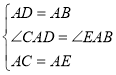∴△CAD≌△EAB（SAS），

∴BE=CD；

（2）BE=CD，理由同（1），

∵四边形ABFD和ACGE均为正方形，

∴AD=AB，AC=AE，∠BAD=∠CAE=90°，

∴∠CAD=∠EAB，

∵在△CAD和△EAB中，

，

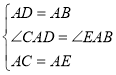∴△CAD≌△EAB（SAS），

∴BE=CD；

（3）由（1）、（2）的解题经验可知，过A作等腰直角△ABD，∠BAD=90°，

则AD=AB=100米，∠ABD=45°，

∴BD=100米，

连接CD，BD，则由（2）可得BE=CD，

∵∠ABC=45°，∴∠DBC=90°，

在Rt△DBC中，BC=100米，BD=100米，

根据勾股定理得：CD==100米，

则BE=CD=100米．