
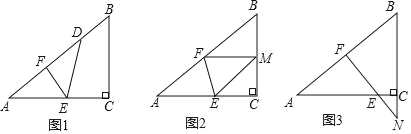
【题目】如图,已知一个三角形纸片ACB,其中∠ACB=90°,AC=8,BC=6,E、F分别是AC、AB边上的点,连接EF.(1)如图1,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=4S△EDF,求ED的长;
(2)如图2,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图3,若FE的延长线与BC的延长线交于点N,CN=2,CE=![]() ,求
,求![]() 的值.
的值.
【答案】(1)2![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)先利用折叠的性质得到![]() ,
, ![]() ≌
≌![]() ,则
,则![]() 则易得S△ABC=5S△AEF,再证明
则易得S△ABC=5S△AEF,再证明![]() 然后根据相似三角形的性质得到
然后根据相似三角形的性质得到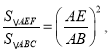 再利用勾股定理求出AB即可得到AE的长;
再利用勾股定理求出AB即可得到AE的长;
(2)①通过证明四条边相等判断四边形AEMF为菱形;
②连结AM交EF于点O,如图②,设![]() 则
则![]() 先证明
先证明![]() 得到
得到![]() 解出
解出![]() 后计算出
后计算出![]() 再利用勾股定理计算出AM,然后根据菱形的面积公式计算EF;
再利用勾股定理计算出AM,然后根据菱形的面积公式计算EF;
(3)如图③,作作![]() 于H,先证明
于H,先证明![]() 利用相似比得到
利用相似比得到![]() 设
设![]() ,则
,则![]()
![]() 再证明
再证明![]() 利用相似比可计算出
利用相似比可计算出![]() 则可计算出
则可计算出![]() 和
和![]() ,接着利用勾股定理计算出
,接着利用勾股定理计算出![]() ,从而得到
,从而得到![]() 的长,于是可计算出
的长,于是可计算出![]() 的值.
的值.
试题解析:(1)∵![]() 的一角沿EF折叠,折叠后点A落在AB边上的点D处,
的一角沿EF折叠,折叠后点A落在AB边上的点D处,
∴![]() ,
, ![]() ≌
≌![]() ,
,
∴![]()
∵S四边形ECBF=![]()
∴S△ABC=5S△AEF,
在Rt ![]() 中,∵
中,∵![]()
∴![]()
∵![]()
∴![]()
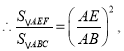
即![]()
∴![]()
由折叠知, ![]()
(2)①连结AM交EF于点O,如图2,

∵![]() 的一角沿EF折叠,折叠后点A落在AB边上的点D处,
的一角沿EF折叠,折叠后点A落在AB边上的点D处,
∴![]()
∵MF∥AC,
∴![]()
∴![]()
∴![]()
∴![]()
∴四边形AEMF为菱形,
②设![]() 则
则![]()
∵四边形AEMF为菱形,
∴EM∥AB,
∴![]()
∴![]()
即![]()
解得![]()
在Rt ![]() 中,
中, ![]()
∵S菱形AEMF![]()
∴![]()
(3)如图③,作![]() 于H,
于H,
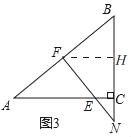
∵EC∥FH,
∴![]()
∴![]()
∴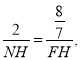
∴![]()
设![]() ,则
,则![]()
![]()
∵FH∥AC,
∴![]()
∴![]()
![]()
∴![]()
∴![]()
在Rt ![]() 中,
中, ![]()
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】某校随机抽取本校部分同学,调查同学了解母亲生日日期的情况,分“知道、不知道、记不清”三种.下面图①、图②是根据采集到的数据,绘制的扇形和条形统计图.

请你要根据图中提供的信息,解答下列问题:
(1)求本次被调查学生的人数,并补全条形统计图;
(2)在图①中,求出“不知道”部分所对应的圆心角的度数;
(3)若全校共有1440名学生,请你估计这所学校有多少名学生知道母亲的生日?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°.
(1)①若∠DCB=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<90°且点E在直线AC的上方时,当这两块三角尺有一组边互相平行时,请直接写出∠ACE角度所有可能的值(不必说明理由).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段a,b,∠α(如图).
(1)以线段a,b为一组邻边作平行四边形,这样的平行四边形能作____个.
(2)以线段a,b为一组邻边,它们的夹角为∠α,作平行四边形,这样的平行四边形能作_____个,作出满足条件的平行四边形(要求仅用直尺和圆规,保留作图痕迹,不写做法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】幻方起源于中国,传说在大禹治水时,有只神龟在洛水中浮起,龟背上有奇特的图案,如图1,人们称之为洛书.如果将龟背上的数字翻译出来,如图2.
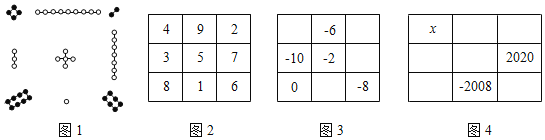
观察发现,图2的每行、每列、每条对角线的三个数之和都是15.像这样,在3×3的方阵图中,每行、每列、每条对角线上3个数的和都相等,我们就称它为三阶幻方.上面的三阶幻方中,15是这个幻方的和,简称幻和.5是幻方最中心的数字,简称中心数.
(1)用﹣10,﹣8,﹣6,﹣4,﹣2,0,2,4,6这九个数字补全图3中的幻方;
(2)如图4是一个三阶幻方,试确定图4中x的值,并给出求解过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB中点,AE∥CD,CE∥AB.
(1)试判断四边形ADCE的形状,并证明你的结论.
(2)连接BE,若∠BAC=30°,CE=1,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
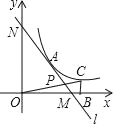
【题目】如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,4),点A为MN的中点,反比例函数y=![]() (x>0)的图象过点A.
(x>0)的图象过点A.
(1)求直线l和反比例函数的解析式;
(2)在函数y=![]() (k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为探测某座山的高度AB,某飞机在空中C处测得山顶A处的俯角为31°,此时飞机的飞行高度为CH=4千米;保持飞行高度与方向不变,继续向前飞行2千米到达D处,测得山顶A处的俯角为50°,求此山的高度AB.(参考数据:tan31°≈0.6,1an50°≈1.2)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式(2x2+ax-y+6)-(2bx22x 5y1).
(1)若多项式的值与字母x的取值无关,求a、b的值.
(2)在(1)的条件下,先化简多项式3(a-ab+b)-(a+ ab+ b),再求它的值.
(3)在(1)的条件下,求(b+a2)+(2b+![]() a2)+(3b+
a2)+(3b+![]() a2)+…+(9b+
a2)+…+(9b+![]() a2)的值.
a2)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com