
ЁОЬтФПЁПНЋвЛИБШ§НЧАхжаЕФСНПщжБНЧШ§НЧАхЕФжБНЧЖЅЕуCАДШчЭМЗНЪНЕўЗХдквЛЦ№ЃЌгбЧщЬсЪОЃКЁЯAЃН60ЁуЃЌЁЯDЃН30ЁуЃЌЁЯEЃНЁЯBЃН45ЁуЃЎ
(1)ЂйШєЁЯDCBЃН45ЁуЃЌдђЁЯACBЕФЖШЪ§ЮЊЁЁ ЁЁЃЎ
ЂкШєЁЯACBЃН140ЁуЃЌдђЁЯDCEЕФЖШЪ§ЮЊЁЁ ЁЁЃЎ
(2)гЩ(1)ВТЯыЁЯACBгыЁЯDCEЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
(3)ЕБЁЯACEЃМ90ЁуЧвЕуEдкжБЯпACЕФЩЯЗНЪБЃЌЕБетСНПщШ§НЧГпгавЛзщБпЛЅЯрЦНааЪБЃЌЧыжБНгаДГіЁЯACEНЧЖШЫљгаПЩФмЕФжЕ(ВЛБиЫЕУїРэгЩ)ЃЎ

ЁОД№АИЁП(1)Ђй135ЁуЃЛЂк40ЁуЃЛ(2)ЁЯACB+ЁЯDCEЃН180ЁуЃЌРэгЩМћНтЮіЃЛ(3)30ЁуЁЂ45ЁуЃЎ
ЁОНтЮіЁП
(1)ЂйИљОнжБНЧШ§НЧАхЕФаджЪНсКЯЁЯDCBЃН45ЁуМДПЩЕУГіЁЯACBЕФЖШЪ§ЃЛ
ЂкгЩЁЯACB=140ЁуЃЌЁЯECB=90ЁуЃЌПЩЕУГіЁЯACEЕФЖШЪ§ЃЌНјЖјЕУГіЁЯDCEЕФЖШЪ§ЃЛ
(2)ИљОнЂйжаЕФНсТлПЩЬсГіВТЯыЃЌдйгЩЁЯACB=ЁЯACD+ЁЯDCBЃЌЁЯACB+ЁЯDCE=90Ёу+ЁЯDCB+ЁЯDCEПЩЕУГіНсТлЃЛ
(3)ЗжCBЁЮADЁЂEBЁЮACСНжжЧщПіНјааЬжТлМДПЩ.
(1)ЂйЁпЁЯDCBЃН45ЁуЃЌЁЯACDЃН90ЁуЃЌ
ЁрЁЯACBЃНЁЯDCB+ЁЯACDЃН45Ёу+90ЁуЃН135ЁуЃЌ
ЙЪД№АИЮЊЃК135ЁуЃЛ
ЂкЁпЁЯACBЃН140ЁуЃЌЁЯECBЃН90ЁуЃЌ
ЁрЁЯACEЃН140ЁуЉ90ЁуЃН50ЁуЃЌ
ЁрЁЯDCEЃН90ЁуЉЁЯACEЃН90ЁуЉ50ЁуЃН40ЁуЃЌ
ЙЪД№АИЮЊЃК40ЁуЃЛ
(2)ВТЯыЃКЁЯACB+ЁЯDCEЃН180ЁуЃЌ
РэгЩШчЯТЃКЁпЁЯACEЃН90ЁуЉЁЯDCEЃЌ
гжЁпЁЯACBЃНЁЯACE+90ЁуЃЌ
ЁрЁЯACBЃН90ЁуЉЁЯDCE+90ЁуЃН180ЁуЉЁЯDCEЃЌ
МДЁЯACB+ЁЯDCEЃН180ЁуЃЛ
(3)30ЁуЁЂ45ЁуЃЎ
РэгЩЃКЕБCBЁЮADЪБЃЈШчЭМ1ЃЉЃЌ
ЁрЁЯAFC=ЁЯFCB=90ЁуЃЌ
ЁпЁЯA=60ЁуЃЌ
ЁрЁЯACEЃН90Ёу-ЁЯA=30ЁуЃЛ
ЕБEBЁЮACЪБЃЈШчЭМ2ЃЉЃЌ
ЁрЁЯACEЃНЁЯE=45ЁуЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫШУИќЖрЕФОгУёЯэЪмУтЗбЕФЬхг§НЁЩэЗўЮёЃЌжиЧьЪаНЋТНајНЈГЩЖрИіЩчЧјНЁЩэЕуЃЌФГЩчЧјЮЊСЫСЫНтНЁЩэЕуЕФЪЙгУЧщПіЃЌЯжЫцЛњЕїВщСЫВПЗжЩчЧјОгУёЃЌНЋЕїВщНсЙћЗжГЩЫФРрЃЌAЃКУПЬьНЁЩэЃЛBЃКОГЃНЁЩэЃЛCЃКХМЖћНЁЩэЃЛDЃКДгВЛНЁЩэЃЛВЂНЋЕїВщНсЙћЛцжЦГЩвдЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭГМЦЭМЃЌНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉБОДЮЕїВщжаЃЌвЛЙВЕїВщСЫ________УћЩчЧјОгУёЃЌЦфжаa=________ЃЛЧыНЋелЯпЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉЮЊСЫЮќв§ИќЖрЩчЧјОгУёВЮМгНЁЩэЃЌНЁЩэЕузМБИОйАьвЛДЮНЁЩэНВзљХрбЕЃЌЮЊДЫЃЌЯыДгБЛЕїВщЕФAРрКЭDРрОгУёжаЗжБ№бЁШЁвЛЮЛдкНВзљЩЯНјааНЛСїЃЌЧыгУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈСаГіЫљгаЕШПЩФмЕФНсЙћЃЌВЂЧѓГіЫљбЁСНЮЛОгУёЧЁКУЪЧвЛЮЛФаадКЭвЛЮЛХЎадЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() бгГЄЯпЩЯвЛЕуЃЌЕу
бгГЄЯпЩЯвЛЕуЃЌЕу![]() дк
дк![]() ЩЯЃЎЧв
ЩЯЃЎЧв![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌдђ
ЃЌдђ![]() ЖШЪ§ЮЊ______ЃЎ
ЖШЪ§ЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮ![]() жаЃЌ
жаЃЌ![]() Еу
Еу![]() ЪЧОиаЮ
ЪЧОиаЮ![]() ФквЛЖЏЕуЃЌЧв
ФквЛЖЏЕуЃЌЧв![]() ЃЌдђ
ЃЌдђ![]() ЕФзюаЁжЕЮЊ_____ЃЎ
ЕФзюаЁжЕЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫФИіКЏЪ§ЃК
Ђйy=kxЃЈkЮЊГЃЪ§ЃЌkЃО0ЃЉ
Ђкy=kx+bЃЈkЃЌbЮЊГЃЪ§ЃЌkЃО0ЃЉ
Ђлy=![]() ЃЈkЮЊГЃЪ§ЃЌkЃО0ЃЌxЃО0ЃЉ
ЃЈkЮЊГЃЪ§ЃЌkЃО0ЃЌxЃО0ЃЉ
Ђмy=ax2ЃЈaЮЊГЃЪ§ЃЌaЃО0ЃЉ
ЦфжаЃЌКЏЪ§yЕФжЕЫцзХxжЕЕУдіДѓЖјМѕЩйЕФЪЧЃЈЁЁЁЁЃЉ
A. Ђй B. Ђк C. Ђл D. Ђм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛЬѕгцДЌФГЪБПЬдкЮЛжУAЙлВтЕЦЫўBЁЂCЃЈЕЦЫўBОрРыAДІНЯНќЃЉЃЌСНИіЕЦЫўЧЁКУдкББЦЋЖЋ65Ёу45ЁфЕФЗНЯђЩЯЃЌгцДЌЯђе§ЖЋЗНЯђКНааlаЁЪБ45ЗжжгжЎКѓЕНДяDЕуЃЌЙлВтЕНЕЦЫўBЧЁКУдке§ББЗНЯђЩЯЃЌвбжЊСНИіЕЦЫўжЎМфЕФОрРыЪЧ12КЃРяЃЌгцДЌЕФЫйЖШЪЧ16КЃРя/ЪБЃЌгжжЊдкЕЦЫўCжмЮЇ18.6КЃРяФкгаАЕНИЃЌЮЪетЬѕгцДЌАДдРДЕФЗНЯђМЬајКНааЃЌгаУЛгаДЅНИЕФЮЃЯеЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
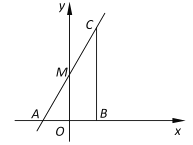
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкжБНЧзјБъЦНУцжаЃЌЕу![]() дк
дк![]() жсЕФИКАыжсЩЯЃЌжБЯп
жсЕФИКАыжсЩЯЃЌжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌгы
ЃЌгы![]() жсЯрНЛгкЕу
жсЯрНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЪЧЕу
ЪЧЕу![]() ЙигкдЕуЕФЖдГЦЕуЃЌЙ§Еу
ЙигкдЕуЕФЖдГЦЕуЃЌЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() жсЃЌНЛжБЯп
жсЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌШчЙћ
ЃЌШчЙћ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжБЯп![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЙћЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЪЧЕШбќШ§НЧаЮЃЌЧыЧѓГіЕу
ЪЧЕШбќШ§НЧаЮЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊABЁЮCDВЛЬэМгШЮКЮзжФИКЭЪ§зжЃЌЧыФудйЬэМгвЛИіЬѕМўЁЯ1=ЁЯ2ГЩСЂ(вЊЧѓИјГіШ§ИіД№АИ)ЃЌВЂбЁдёЦфжавЛжжЧщПіМгвджЄУї.

ЬѕМў1ЃК________________________________ЃЛ
ЬѕМў2ЃК________________________________ЃЛ
ЬѕМў3ЃК________________________________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌХзЮяЯп![]() ЃЈ aЁй0ЃЉОЙ§дЕуЃЌЖЅЕуЮЊAЃЈhЃЌkЃЉЃЈhЁй0ЃЉЃЎ
ЃЈ aЁй0ЃЉОЙ§дЕуЃЌЖЅЕуЮЊAЃЈhЃЌkЃЉЃЈhЁй0ЃЉЃЎ
ЃЈ1ЃЉЕБhЃН1ЃЌkЃН2ЪБЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєХзЮяЯп![]() ЃЈtЁй0ЃЉвВОЙ§AЕуЃЌЧѓaгыtжЎМфЕФЙиЯЕЪНЃЛ
ЃЈtЁй0ЃЉвВОЙ§AЕуЃЌЧѓaгыtжЎМфЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉЕБЕуAдкХзЮяЯп![]() ЩЯЃЌЧвЃ2ЁмhЃМ1ЪБЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ЩЯЃЌЧвЃ2ЁмhЃМ1ЪБЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com