
 如图,AD是△ABC的中线,AB=
如图,AD是△ABC的中线,AB=| 37 |
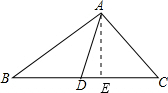 解:如图,过A作AE⊥BC于点E,
解:如图,过A作AE⊥BC于点E,| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 37 |
| AE |
| EC |
2
| ||
| 1 |
| 3 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
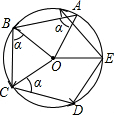 如图所示,小范从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小范第五次走到场地边缘时处于弧AB上,此时∠AOE=48°,则α的度数是( )
如图所示,小范从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小范第五次走到场地边缘时处于弧AB上,此时∠AOE=48°,则α的度数是( )| A、60° | B、51° |
| C、48° | D、76° |
查看答案和解析>>
科目:初中数学 来源: 题型:
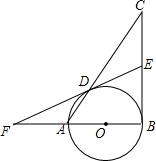 如图,在△ABC中,∠ABC=90°,AB=4,BC=5,以AB为直径的⊙O交AC于点D,点E是BC的中点,连接ED并延长交BA的延长线于点F.
如图,在△ABC中,∠ABC=90°,AB=4,BC=5,以AB为直径的⊙O交AC于点D,点E是BC的中点,连接ED并延长交BA的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
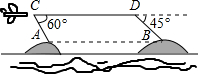 某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得你正前方一海岛顶端A的俯角是60°,然后沿平行与AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是45°,求两海岛间的距离AB.
某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得你正前方一海岛顶端A的俯角是60°,然后沿平行与AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是45°,求两海岛间的距离AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com