
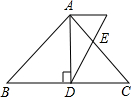
 如图,AD是等腰△ABC底边上的高,且AD=4,sinB=$\frac{4}{5}$,若E是AC边上的点,且满足AE:EC=2:3,连接DE,求cot∠ADE的值.
如图,AD是等腰△ABC底边上的高,且AD=4,sinB=$\frac{4}{5}$,若E是AC边上的点,且满足AE:EC=2:3,连接DE,求cot∠ADE的值. 分析 作AF∥BC交DE的延长线于F,如图,根据等腰三角形的性质得BD=CD,AB=AC,在Rt△ABD中利用∠B的正弦可求出AB=5,再利用勾股定理可计算出BD=3,所以CD=3,AC=5,然后通过△AEF∽△CED,利用相似比可计算出AF=2,然后在Rt△DAF中,根据余切的定义求解.
解答 解:作AF∥BC交DE的延长线于F,如图,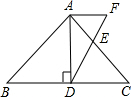
∵AD是等腰△ABC底边上的高,
∴BD=CD,AB=AC,
在Rt△ABD中,∵sinB=$\frac{AD}{AB}$=$\frac{4}{5}$,而AD=4,
∴AB=5,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=3,
∴CD=3,AC=5,
∵AF∥CD,
∴∠DAF=90°,△AEF∽△CED,
∴$\frac{AF}{CD}$=$\frac{AE}{EC}$,即$\frac{AF}{3}$=$\frac{2}{3}$,
∴AF=2,
在Rt△DAF中,cot∠ADF=$\frac{AD}{AF}$=$\frac{4}{2}$=2,
即cot∠ADE的值为2.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了相似三角形的判定与性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 按要求作图并回答问题:
按要求作图并回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
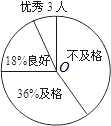 李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.
李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.| 综合素质 | 考试成绩 | 体育测试 | |
| 满分 | 100 | 100 | 100 |
| 小聪 | 72 | 98 | 60 |
| 小亮 | 90 | 75 | 95 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=2BD.则实数k的值为4$\sqrt{3}$.
如图,若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=2BD.则实数k的值为4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
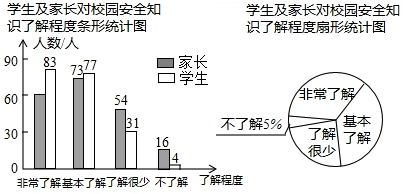
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com