
分析 根据已知假设每盆花苗(原来花盆中有3株)增加a(a为偶数)株,盈利为y元,则每盆花苗有(a+3)株,得出平均单株盈利为(3-0.5×$\frac{a}{2}$)元,由题意得y=(a+3)(3-0.5×$\frac{a}{2}$),根据二次函数的性质即可求得.
解答 解:设每盆花苗(假设原来花盆中有3株)增加a(a为偶数)株,盈利为y元,
则根据题意得:y=(3-0.5×$\frac{a}{2}$)(a+3)
=-$\frac{1}{4}$(a-$\frac{9}{2}$)2+$\frac{225}{16}$,
∵a为偶数,
∴a=4,
∵当a=2时,y=12.5<13
当a=4时,y=(2-0.5×$\frac{4}{2}$)+(4+3)=14>13,
当a=6时,y=(2-0.5×$\frac{6}{2}$)+(6+3)=13.5>13,
∴每盆植7株时能使单盆取得最大盈利;若需要单盆盈利不低于13元,则每盆需要植7或9株.
故答案为7、7或9.
点评 此题考查了二次函数的应用,根据每盆花苗株数×平均单株盈利=总盈利得出方程是解题关键.


科目:初中数学 来源:2016-2017学年度海南省九年级第二次月考数学试卷(解析版) 题型:单选题
在正方形网格中,△ABC的位置如图所示,则cosB的值为( )
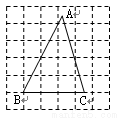
A. 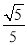 B.
B. 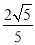 C.
C. 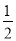 D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 水果品种 | A | B | C |
| 每辆汽车运装量/t | 4 | 3 | 2 |
| 每吨水果获利/百元 | 6 | 8 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
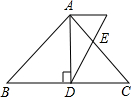 如图,AD是等腰△ABC底边上的高,且AD=4,sinB=$\frac{4}{5}$,若E是AC边上的点,且满足AE:EC=2:3,连接DE,求cot∠ADE的值.
如图,AD是等腰△ABC底边上的高,且AD=4,sinB=$\frac{4}{5}$,若E是AC边上的点,且满足AE:EC=2:3,连接DE,求cot∠ADE的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
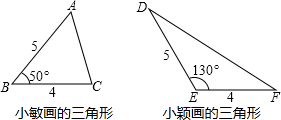
| A. | S△ABC>S△DEF | B. | S△ABC<S△DEF | C. | S△ABC=S△DEF | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10个 | B. | 15个 | C. | 20个 | D. | 25个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com