
| 水果品种 | A | B | C |
| 每辆汽车运装量/t | 4 | 3 | 2 |
| 每吨水果获利/百元 | 6 | 8 | 5 |
分析 (1)关键描述语:某乡组织30辆汽车装运A、B、C三种水果共84吨到外地销售,根据每辆汽车运装量和汽车的辆数,可列出y与x之间的函数关系式,再根据装运每种水果的汽车不少于4辆,装运的B种水果的重量不超过装运的A、C两种水果重量之和.
可将自变量x的取值范围求出;
(2)根据水果品种每吨水果的利润和销售的数量,可将此次外销活动的利润Q表示出来,根据x的取值范围,从而将最大利润时车辆的分配方案求出.
解答 解:(1)由题得到:4x+3y+2(30-x-y)=84,所以y=-2x+24,
又因为x≥4,y≥4,30-x-y≥4,
则-2x+24≥4,30-x-(-2x+24)≥4,
得到-2≤x≤10;
∵y≤x+30-x-y,y=-2x+24,
∴x≥4.5,
∴4.5≤x≤10;
(2)Q=6×4x+8×3y+5×2(30-x-y)=-6x+540,
Q随着x的减小而增大,又因为4.5≤x≤10,所以当x=5时,Q取得最大值,即Q=5×4×6+14×3×8+11×2×5(元)=566(百元),
此时应这样安排:A水果用5辆车,B水果用14辆车,C水果用11辆车.
点评 本题主要考查一次函数在实际生活中的应用,在解题过程中应确定未知量的取值范围.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源:2016-2017学年度海南省九年级第二次月考数学试卷(解析版) 题型:单选题
如图,在矩形ABCD中,对角线AC、BD交于点O,OE⊥BD交AB于E,若∠ABD=30°,DE=6,则矩形ABCD的周长为( )
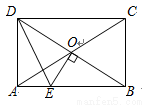
A. 6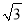 +18 B. 3
+18 B. 3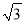 +9 C. 2
+9 C. 2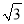 +18 D.
+18 D. 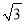 +9
+9
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.
李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.| 综合素质 | 考试成绩 | 体育测试 | |
| 满分 | 100 | 100 | 100 |
| 小聪 | 72 | 98 | 60 |
| 小亮 | 90 | 75 | 95 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分数段 | 人数(人) | 频率 |
| A | 48 | 0.48 |
| B | a | 0.32 |
| C | b | 0.10 |
| D | c | d |
| E | e | 0.05 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com