
分析 (1)根据不了解的人数除以不了解的人数所占的百分比,可得答案;
(2)根据圆周角乘以基本了解所占的百分比,可得答案;
(3)根据观察条形统计图,可得答案;
(4)根据了解很少的学生人数比上抽测的学生人数,可得答案.
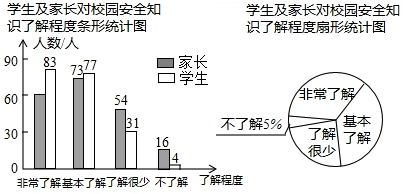
解答 解:(1)参与调查的学生及家长一共有(16+4)÷5%=400人;
(2)在扇形统计图中,“基本了解”所对应的圆心角度数是360°×$\frac{73+77}{400}$=135°;
(3)在条形统计图中,“非常了解”所对应的学生人数是83人;
故答案为:400,315°,83;
(4)从这次接受调查的学生中,随机抽查一个,恰好是“了解很少”的学生的概率是p=$\frac{31}{83+77+31+4}$=$\frac{31}{195}$.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:解答题
| 水果品种 | A | B | C |
| 每辆汽车运装量/t | 4 | 3 | 2 |
| 每吨水果获利/百元 | 6 | 8 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
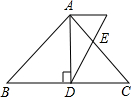 如图,AD是等腰△ABC底边上的高,且AD=4,sinB=$\frac{4}{5}$,若E是AC边上的点,且满足AE:EC=2:3,连接DE,求cot∠ADE的值.
如图,AD是等腰△ABC底边上的高,且AD=4,sinB=$\frac{4}{5}$,若E是AC边上的点,且满足AE:EC=2:3,连接DE,求cot∠ADE的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
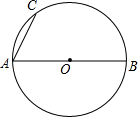 如图,AB是⊙O的直径,AC为弦.
如图,AB是⊙O的直径,AC为弦.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
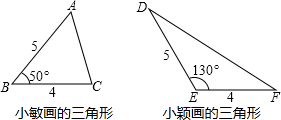
| A. | S△ABC>S△DEF | B. | S△ABC<S△DEF | C. | S△ABC=S△DEF | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
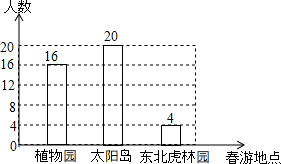 某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.
某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com