
| A. | 75°或15° | B. | 75° | C. | 15° | D. | 75°或30° |
分析 因为三角形的高有三种情况,而直角三角形不合题意,故舍去,所以应该分两种情况进行分析,从而得到答案.
解答 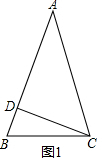 解:当等腰三角形是锐角三角形时,如图1所示
解:当等腰三角形是锐角三角形时,如图1所示
∵CD⊥AB,CD=$\frac{1}{2}$AC,
∴sin∠A=$\frac{CD}{AD}$=$\frac{1}{2}$,
∴∠A=30°,
∴∠B=∠ACB=75°;
当等腰三角形是钝角三角形时,如图2示,
∵CD⊥AB,即在直角三角形ACD中,CD=$\frac{1}{2}$AC,
∴∠CAD=30°,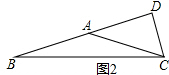
∴∠CAB=150°,
∴∠B=∠ACB=15°.
故其底角为15°或75°.
故选A.
点评 此题主要考查等腰三角形的性质,含30°的角的直角三角形的性质,在解决与等腰三角形有关的问题,由于等腰所具有的特殊性质,很多题目在已知不明确的情况下,要进行分类讨论,才能正确解题,因此,解决和等腰三角形有关的边角问题时,要仔细认真,避免出错.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
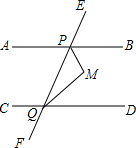 如图,直线EF与直线AB,CD分别相交于点P,Q,∠EPB=x°,∠CQP=180°-x°,PM平分∠BPQ,QM平分∠PQD,判断PM与QM之间的位置关系,并说明理由.
如图,直线EF与直线AB,CD分别相交于点P,Q,∠EPB=x°,∠CQP=180°-x°,PM平分∠BPQ,QM平分∠PQD,判断PM与QM之间的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
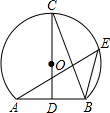 如图,点E是$\widehat{ACB}$上一动点,点D是弦AB的中点,CD经过圆心O,则下列结论中不一定正确的是( )
如图,点E是$\widehat{ACB}$上一动点,点D是弦AB的中点,CD经过圆心O,则下列结论中不一定正确的是( )| A. | CD⊥AB | B. | ∠AEB=2∠BCD | C. | ∠BAE<∠CBE | D. | $\widehat{AC}$=$\widehat{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
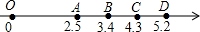 如图,在数轴上有标有O,A,B,C,D五个点,根据图中各点所表示的数,$\sqrt{12}$在线段( )
如图,在数轴上有标有O,A,B,C,D五个点,根据图中各点所表示的数,$\sqrt{12}$在线段( )| A. | OA上 | B. | AB上 | C. | BC上 | D. | CD上 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com