
分析 (1)根据二次函数的根的判别式△=b2-4ac的符号来判断方程的根的情况;
(2)由(1)知原方程有两个实数根,所以根据求根公式和已知条件“m≠0,x1>x2”求得x1、x2的值,并将其代入且$y=1-\frac{x_2}{x_1}$,求得这个函数的解析式.
解答 解:(1)由题意有△=[-(2m-1)]2-4(m2-m)=1>0.
∴不论m取何值时,方程总有两个不相等的实数根;
(2)方程的两个实数根分别为x1,x2(其中x1>x2),
解关于x的一元二次方程x2-(2m-1)x+m2-m=0可得x1=m,x2=m-1,
则$y=1-\frac{x_2}{x_1}=1-\frac{m-1}{m}=\frac{1}{m}$.
点评 本题考查了根与系数的关系、根的判别式,熟练掌握根与系数的关系、根的判别式是解题的关键.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
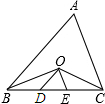 已知,如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=8cm,则△ODE的周长为8cm.
已知,如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=8cm,则△ODE的周长为8cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
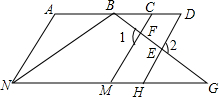 如图,∠1=∠2,∠D=∠CMG.
如图,∠1=∠2,∠D=∠CMG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com