Question

13．如图所示，AB是⊙O的直径，CD是⊙O的弦，AE⊥CD，BF⊥CD，垂足分别为点E、F，AB=20，CD=16．
（1）求证：AE+BF=12；
（2）当AB与CD在⊙O内相交时，设交点为N，（1）中的结论是否成立？若成立，加以证明；若不成立，请写出新结论，并加以证明．

Answer 1

分析 （1）连接OC，由AB=20，CD=16，即可推出CM和OC的长度，然后由勾股定理求得OM的长度，然后由OM是梯形AEFB中位线，根据梯形中位线的性质即可推出AE+BF=2OM=12．
（2）连接OC、BE，作OH⊥CD，交CD于G，交BE于H，根据勾股定理确定OG=6，根据三角形中位线确定OH=$\frac{1}{2}$AE，HG=$\frac{1}{2}$AF，根据OH-GH=OG=$\frac{1}{2}$AE-$\frac{1}{2}$BF，即可求得AE-BF=12．

解答 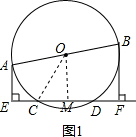（1）证明：连接OC，作OM⊥CD于M，
∵AB=20，
∴OC=$\frac{1}{2}$AB=10，
∵OM⊥CD，CD=16，
∴CM=$\frac{1}{2}$CD=8，
∵Rt△OCM，
∴OM=$\sqrt{O{C}^{2}-C{M}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6，
∵OA=OB，ME=MF，
∴OM是梯形AEFB中位线，
∴AE+BF=2OM=12，
（2）（1）中的结论不成立，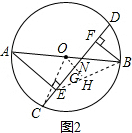
证明：连接OC、BE，作OH⊥CD，交CD于G，交BE于H，
则∠OGC=90°，且CG=DG=8，且OH∥AE，GH∥BF，
∴OG=$\sqrt{O{C}^{2}-C{N}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6，
∵O是AB的中点，
∴OH=$\frac{1}{2}$AE，HG=$\frac{1}{2}$AF，
∴OH-GH=OG=$\frac{1}{2}$AE-$\frac{1}{2}$BF，
∴AE-BF=12．

点评 本题主要考查垂径定理，平行线的性质，勾股定理等知识点，关键在于根据题意正确的做出辅助线，熟练运用相关的性质定理，认真的进行计算．