
分析 (1)首先用计算器分别求出$\sqrt{18}$与$\root{3}{35}$的值各是多少;然后根据实数大小比较的方法判断即可.
(2)首先用计算器分别求出$\frac{8}{13}$与$\frac{\sqrt{6}-1}{2}$的值各是多少;然后根据实数大小比较的方法判断即可.
解答 解:(1)$\sqrt{18}$≈4.24,$\root{3}{35}$≈3.27,
∵4.24>3.27,
∴$\sqrt{18}$>$\root{3}{35}$.
(2)$\frac{8}{13}$≈0.615,$\frac{\sqrt{6}-1}{2}$≈$\frac{2.449-1}{2}$=0.7245,
∵0.615<0.7245,
∴$\frac{8}{13}$<$\frac{\sqrt{6}-1}{2}$.
点评 此题主要考查了计算器-数的开方问题,以及实数大小比较的方法,要熟练掌握.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
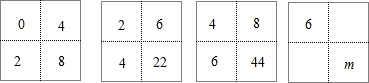
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
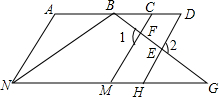 如图,∠1=∠2,∠D=∠CMG.
如图,∠1=∠2,∠D=∠CMG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com