Question

6．已知在菱形ABCD中，∠BAD=60°，P是形内一点，且PD=1，PA=$\sqrt{3}$，PB=2，则PC=3．

Answer 1

分析 根据菱形的性质得AD=AB=CD，而∠BAD=60°，则将△ABP绕点A逆时针性质60°得△ADE，连结PE，如图，根据旋转的性质得AP=AE=$\sqrt{3}$，DE=PB=2，∠EAP=60°，∠AED=∠APB，则可判断△AEP为等边三角形，所以PE=AP=$\sqrt{3}$，∠APE=∠PEA=60°，于是可根据勾股定理判断△PDE为直角三角形，∠DPE=90°，且∠DEP=30°，所以∠AED=90°=∠APB，利用周角为360°可计算出∠BPD=120°，加上∠BCD=60°，所以可判断B、C、D、P四点共圆，连结BD，在PC上截取PF=PD=1，如图，接着证明△BCD为等边三角形得到∠DBC=∠BDC=60°，DB=DC，根据圆周角定理得∠DPC=∠DBC=60°，则可判断△PDF为等边三角形，得到∠PDF=60°，根据旋转的定义，可把△DFC绕点D顺时针旋转60°得到△DPB，则CF=PB=2，于是得到PC=PF+CF=3．

解答 解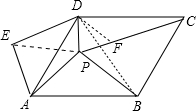：∵四边形ABCD为菱形，
∴AD=AB=CD，
而∠BAD=60°，
将△ABP绕点A逆时针旋转60°得△ADE，连结PE，如图，
∴AP=AE=$\sqrt{3}$，DE=PB=2，∠EAP=60°，∠AED=∠APB，
∴△AEP为等边三角形，
∴PE=AP=$\sqrt{3}$，∠APE=∠PEA=60°，
在△PDE中，∵PD=1，PE=$\sqrt{3}$，DE=2，
∴PD²+PE²=DE²，
∴△PDE为直角三角形，∠DPE=90°，
∴∠DEP=30°，
∴∠AED=30°+60°=90°，
∴∠APB=90°，
∴∠BPD=360°-90°-90°-60°=120°，
∵四边形ABCD为菱形，
∴∠BCD=60°，
∴∠BPD+∠BCD=180°，
∴B、C、D、P四点共圆，
连结BD，在PC上截取PF=PD=1，如图，
∵四边形ABCD为菱形，∠BCD=60°，
而CD=CB，
∴△BCD为等边三角形，
∴∠DBC=∠BDC=60°，DB=DC，
∴∠DPC=∠DBC=60°，
∴△PDF为等边三角形，
∴∠PDF=60°，
∴△DFC绕点D顺时针旋转60°可得到△DPB，
∴CF=PB=2，
∴PC=PF+CF=1+2=3．

点评 本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．也考查了旋转的性质、等边三角形的判定与性质和勾股定理的逆定理．