
【题目】如图,正方形![]() 和
和![]() 的边
的边![]() ,
,![]() 在同一条直线上,且
在同一条直线上,且![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
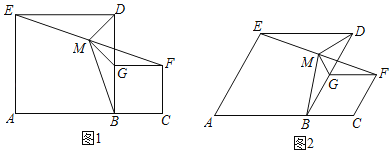
(1)试证明![]() ,并求
,并求![]() 的值.
的值.
(2)如图,将如图中的正方形变为菱形,设![]() ,其它条件不变,问(1)中
,其它条件不变,问(1)中![]() 的值有变化吗?若有变化,求出该值(用含
的值有变化吗?若有变化,求出该值(用含![]() 的式子表示);若无变化,说明理由.
的式子表示);若无变化,说明理由.
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,则:AC=![]() AB.
AB.

探究结论:小明同学对以上结论作了进一步研究.
(1)如图1,连接AB边上中线CE,由于CE=![]() AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
(2)如图2,点D是边CB上任意一点,连接AD,作等边△ADE,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系,写出你的猜想并加以证明.
(3)当点D为边CB延长线上任意一点时,在(2)条件的基础上,线段BE与DE之间存在怎样的数量关系?请直接写出你的结论 .
拓展应用:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣![]() ,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某品牌太阳能热水器的侧面示意图.已知铁架水平横管![]() 平行于水平线AD,长为
平行于水平线AD,长为![]() 的真空管
的真空管![]() 与水平线
与水平线![]() 的夹角为37°,铁架
的夹角为37°,铁架![]() 的倾斜角
的倾斜角![]() 为22°,铁架竖直管
为22°,铁架竖直管![]() 的长度为05
的长度为05 ![]() ,根据以上信息,请求出:
,根据以上信息,请求出:

(1))真空管上端![]() 到水平线
到水平线![]() 的距离;
的距离;
(2)水平横管![]() 的长度(结果精确到0.1
的长度(结果精确到0.1 ![]() )(参考数据:
)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
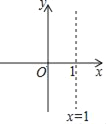
【题目】在平面直角坐标系中,抛物线y=x2﹣2x+c(c为常数)的对称轴如图所示,且抛物线过点C(0,c).
(1)当c=﹣3时,点(x1,y1)在抛物线y=x2﹣2x+c上,求y1的最小值;
(2)若抛物线与x轴有两个交点,自左向右分别为点A、B,且OA=![]() OB,求抛物线的解析式;
OB,求抛物线的解析式;
(3)当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
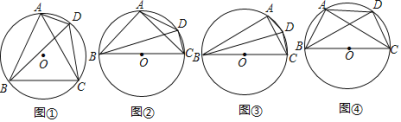
【题目】(1)方法选择
如图①,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() ,
,![]() .求证:
.求证:![]() .
.
小颖认为可用截长法证明:在![]() 上截取
上截取![]() ,连接
,连接![]() …
…
小军认为可用补短法证明:延长![]() 至点
至点![]() ,使得
,使得![]() …
…
请你选择一种方法证明.
(2)类比探究
(探究1)
如图②,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() .试用等式表示线段
.试用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
(探究2)
如图③,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() .若
.若![]() 是
是![]() 的直径,
的直径,![]() ,则线段
,则线段![]() ,
,![]() ,
,![]() 之间的等量关系式是______.
之间的等量关系式是______.
(3)拓展猜想
如图④,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() .若
.若![]() 是
是![]() 的直径,
的直径,![]() ,则线段
,则线段![]() ,
,![]() ,
,![]() 之间的等量关系式是______.
之间的等量关系式是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
频数频率分布表
成绩x(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,有下列结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△ADE的周长是9.其中,正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.
(1)若购买这两类球的总金额为4600元,求篮球、足球各买了多少个?
(2)若购买篮球的总金额不超过购买足球的总金额,求最多可购买多少个篮球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com