
����Ŀ���������龳�����ۺ�ʵ�����ϣ�ͬѧ������ͼ�ε�ƽ����Ϊ���չ��ѧ�����ͼ�٣��Ƚ�һ�ų�Ϊ4����Ϊ3�ľ���ֽƬ�ضԽ�������ƴ����ͼ��ʾ���ı���![]() ��
��![]() ��
��![]() ����ƴ�õ��ı���
����ƴ�õ��ı���![]() ���ܳ���_____.
���ܳ���_____.

���������֣���ͼ���е�![]() ��������
��������![]() ����ƽ�ƣ�����
����ƽ�ƣ�����![]() ��
��![]() ��
��![]() ��
��![]() ����ͼ��.��
����ͼ��.��![]() ��ƽ�ƾ�����
��ƽ�ƾ�����![]() �ij���ʱ�����ı���
�ij���ʱ�����ı���![]() ���ܳ�.
���ܳ�.
������̽������ͼ���е�![]() ������������
������������![]() ����ƽ�ƣ������������䣬���ı���
����ƽ�ƣ������������䣬���ı���![]() ������ʱ�����ı���
������ʱ�����ı���![]() �ضԽ��������õõ����ĸ�������ƴ�����������ȵľ��Σ�ֱ��д�����п���ƴ�ɵľ����ܳ�.
�ضԽ��������õõ����ĸ�������ƴ�����������ȵľ��Σ�ֱ��д�����п���ƴ�ɵľ����ܳ�.
���𰸡��������龳��16�����������֡�6+2![]() ��������̽����20��22��
��������̽����20��22��
��������
�������龳��
���������⣬�ɵ�AB=CD��AC=BD����ADB=��DBC=90����Ȼ����ݹ��ɶ������ɵ�AB����������ı���ABCD���ܳ���
���������֡�
������ƽ�ƣ���AE=CF=3��DE=BF���ٸ���ƽ�У������ж��ı���AECF��ƽ���ı��Σ�Ȼ����ݹ��ɶ������ɵ�AF����������ı���AECF���ܳ���
������̽����
������ƽ�ƣ��õ���E���F�غ�ʱ���ı���ABCDΪ���Σ��ó���Խ��ߵij����ضԽ���������������ɵľ����������������6Ϊ����4Ϊ���ľ��κ���3Ϊ����8Ϊ���ľ��Σ�����������ܳ�.
�����⣬�ɵ�AB=CD��AC=BD����ADB=��DBC=90��
����![]() ��
��![]() ��
��
����ݹ��ɶ������ɵ�![]()
���ı���![]() ���ܳ���
���ܳ���![]()
�ʴ�Ϊ16.
��ƽ�ƣ���AE=CF=3��DE=BF��
��AE��CF��
���ı���AECF��ƽ���ı��Σ�
��BE=DF=4��
��EF=DE=2��
��Rt��AEF����AEF=90����
�ɹ��ɶ�������AF=![]() =
=![]() ��
��
���ı���AECF���ܳ�Ϊ2AE+2AF=6+2![]() ��
��
��ƽ�ƣ��õ���E���F�غ�ʱ���ı���ABCDΪ���Σ�AE=CE=3��BE=DE=4���ضԽ���������������ɵľ��������������
����6Ϊ����4Ϊ���ľ��Σ����ܳ�Ϊ![]() ��
��
����3Ϊ����8Ϊ���ľ��Σ����ܳ�Ϊ![]() .
.
�ʴ�Ϊ20��22��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������������ݣ���������⣺
����˼����С����ѧϰ��ʵ����һ�º��Լ�̽������������������ۣ�
��![]() ��
��![]() ��
��![]() ��
��![]() ����9��4������ƽ������
����9��4������ƽ������
��9��4������ƽ����ֻ��һ��������![]() =
=![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��![]() ����9��16������ƽ������
����9��16������ƽ������
��9��16������ƽ����ֻ��һ��������������
�����������⣺
��1������բٰ���С����ɢڵ���գ������룺һ��أ���a��0��b��0ʱ��![]() ��
��![]() ��
��![]() ֮��Ĵ�С��ϵ�������ģ�
֮��Ĵ�С��ϵ�������ģ�
��2���پ�һ�����ӣ����������Ľ���Ƿ���ȷ��
��3���������Ͻ��ۣ����㣺![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ҹ�������ѧ����ԣ�Լ13���ͣ������ġ���������������1261�꣩һ���У�����ͼ�������ν��Ͷ���͵ij˷����ɣ������ע�����ᵽ������֮ǰ������ѧ�Ҽ��ܣ�1050�����ң�Ҳ�ù�����������������dz����������Ϊ���������������������������������������ϵ�������![]() ������ÿһ����Ϊ���Ϸ������ң������ĺͣ���ʵ�ϣ���������θ�����
������ÿһ����Ϊ���Ϸ������ң������ĺͣ���ʵ�ϣ���������θ�����![]()
![]() ��չ��ʽ����
��չ��ʽ����![]() �Ĵ����ɴ�С��˳��ϵ�����ɣ����磬���������е����е�
�Ĵ����ɴ�С��˳��ϵ�����ɣ����磬���������е����е�![]() ����
����![]() ��ǡ�ö�Ӧ��
��ǡ�ö�Ӧ��![]() չ��ʽ�еĸ���ϵ���������е�
չ��ʽ�еĸ���ϵ���������е�![]() ����
����![]() ��ǡ�ö�Ӧ��
��ǡ�ö�Ӧ��![]() չ��ʽ�еĸ���ϵ�����ȵȣ�������������ܵ���ѧ֪ʶ������������⣺
չ��ʽ�еĸ���ϵ�����ȵȣ�������������ܵ���ѧ֪ʶ������������⣺
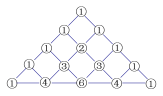
��1��д��![]() ��չ��ʽ��
��չ��ʽ��
��2��������ʽ�ij˷���֤��Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y����![]() x+3��x���ཻ�ڵ�B����y���ཻ�ڵ�A����EΪ�߶�AB�е㣬��ABO��ƽ����BD��y������ڵ�D����A��C���ڵ�O�Գƣ�
x+3��x���ཻ�ڵ�B����y���ཻ�ڵ�A����EΪ�߶�AB�е㣬��ABO��ƽ����BD��y������ڵ�D����A��C���ڵ�O�Գƣ�
��1�����߶�DE�ij���
��2��һ������P�ӵ�D���������ʵ���·���˶���ֱ��BC�ϵĵ�F����������CB�����ƶ�2![]() ����λ����G�����ӵ�G���ʵ���·���˶�����E������P���˶�·�����ʱ�����ʱ��G�����ꣻ
����λ����G�����ӵ�G���ʵ���·���˶�����E������P���˶�·�����ʱ�����ʱ��G�����ꣻ
��3������ADE�Ƶ�A˳ʱ�뷽����ת����ת�Ƕ�����0������180�㣩������ת������DE���ڵ�ֱ�߷ֱ���ֱ��BC��ֱ��AC�ཻ�ڵ�M����N���Ƿ����ijһʱ��ʹ��CMNΪ���������Σ������ڣ������CM�ij����������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������ס������ֻ�����װ�У���֪ͬ����6m�����Ƴɼеĸ������Ƴ��Һеĸ�����2�������Ƴ�һ���б��Ƴ�һ���Һ���Ҫ����20%�IJ��ϣ�
��1��������ÿ���С��Һи��ö����ײ��ϣ�
��2����������ס������ְ�װ�й�3000�����Ҽе������������Һ�������2������ô��д������Ҫ���ϵ��ܳ���l��m���������n������֮��ĺ�����ϵʽ�������������Ҫ�����ײ��ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�![]() ��
��![]() ����G��E�ֱ��ڱ�AB��CD�ϣ���F��H�ڶԽ���AC�ϣ����ı���EFGH�����Σ���AG�ij��ǣ� ��
����G��E�ֱ��ڱ�AB��CD�ϣ���F��H�ڶԽ���AC�ϣ����ı���EFGH�����Σ���AG�ij��ǣ� ��

A.![]() B.5C.
B.5C.![]() D.6
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ�߾�������![]() �ĶԽ���
�ĶԽ���![]() ���е�
���е�![]() ���ֱ�����ε������ཻ�ڵ�
���ֱ�����ε������ཻ�ڵ�![]() ��
��![]() .
.
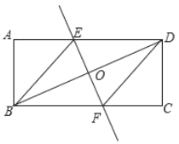
(1)��֤��![]() ��
��
(2)��![]() �����ı���
�����ı���![]() ��______�Σ���˵�����ɣ�
��______�Σ���˵�����ɣ�
(3)��(2)�������£���![]() ��
��![]() ����
����![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУѧ����ɲ���Уѧ���ᳫ��������������Ը������г������飬�õ�һ��ѧ�������������ݣ���ͼ�Ǹ����������ݻ��Ƶ�ͳ��ͼ��ͼ�д����Ҹ������θ߶�֮��Ϊ3��4��5��8��2����֪�˴ε����о�15Ԫ��20Ԫ��������39�ˣ�
��1������һ������˶����˾����������20Ԫ�ĸ����Ƕ��٣�
��2���������ݵ���������λ�����Ƕ��٣�
��3������У����2310��ѧ���������ȫУѧ����������Ԫ��
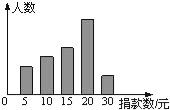
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���峯��ѧ��÷�Ķ��������������ۡ���������һ���⣺ɽ����Ķ��������Ķ������ʵ����Ķ�߷֣���ɽ����Ķ��������Ķ������ʵ����Ķ��֣���ÿĶɽ����ʵ�������
ÿĶ������ʵ�������
����Ϊ��������ɽ��3Ķ������6Ķ��������൱��ʵ��4.7Ķ����ɽ��5Ķ������3Ķ��������൱��ʵ��5.5Ķ����ÿĶɽ���ÿĶ���ز������൱��ʵ�����Ķ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com