
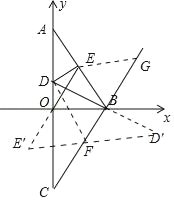
【题目】如图,直线y=﹣![]() x+3与x轴相交于点B,与y轴相交于点A,点E为线段AB中点,∠ABO的平分线BD与y轴相较于点D,点A、C关于点O对称.
x+3与x轴相交于点B,与y轴相交于点A,点E为线段AB中点,∠ABO的平分线BD与y轴相较于点D,点A、C关于点O对称.
(1)求线段DE的长;
(2)一个动点P从点D出发,沿适当的路径运动到直线BC上的点F,再沿射线CB方向移动2![]() 个单位到点G,最后从点G沿适当的路径运动到点E处,当P的运动路径最短时,求此时点G的坐标;
个单位到点G,最后从点G沿适当的路径运动到点E处,当P的运动路径最短时,求此时点G的坐标;
(3)将△ADE绕点A顺时针方向旋转,旋转角度α(0<α≤180°),在旋转过程中DE所在的直线分别与直线BC、直线AC相交于点M、点N,是否存在某一时刻使△CMN为等腰三角形,若存在,请求出CM的长,若不存在,请说明理由.

【答案】(1)1;(2)(![]() ,
,![]() );(3)6+
);(3)6+![]() ﹣3
﹣3![]() 或6+
或6+![]() +3
+3![]() 或2
或2![]() ﹣2或8
﹣2或8![]() .
.
【解析】
(1)想办法证明DE⊥AB,利用角平分线的性质定理证明DE=OD即可解决问题;
(2)过点E作EE′∥BC,点E′在x轴下方且EE′=2![]() ,作点D关于直线BC的对称点D′,连接E′D′交BC于F,在射线CB上取FG=2
,作点D关于直线BC的对称点D′,连接E′D′交BC于F,在射线CB上取FG=2![]() .此时D→F→G→E的路径最短.
.此时D→F→G→E的路径最短.
(3)分三种情形:①如图1中,当CM=CN时,在AE上取一点P,使得AP=PN.设EN=x.②如图2中,当MN=MC时,作BP⊥MN于P,则四边形ADPB是矩形.③如图3中,当NC=MN时,D与N重合,作DP⊥BC于P.分别解直角三角形即可解决问题.
解:(1)∵直线y=﹣![]() x+3与x轴相交于点B,与y轴相交于点A,
x+3与x轴相交于点B,与y轴相交于点A,
∴A(0,3),B(![]() ,0),
,0),
∴OA=3,OB=![]() ,
,
∴tan∠ABO=![]() =
=![]() ,
,
∴∠ABO=60°,
∵BD平分∠ABO,
∴∠DBO=30°,
∴OD=OBtan30°=1,DB=2OD=2,
∴AD=DB=2,
∴AE=EB,
∴DE⊥AB,∵DO⊥OB,DB平分∠ABO,
∴DE=DO=1.
(2)过点E作EE′∥BC,点E′在x轴下方且EE′=2![]() ,作点D关于直线BC的对称点D′,连接E′D′交BC于F,在射线CB上取FG=2
,作点D关于直线BC的对称点D′,连接E′D′交BC于F,在射线CB上取FG=2![]() .此时D→F→G→E的路径最短.
.此时D→F→G→E的路径最短.
∵E′(![]() ,
,![]() ),D′(2
),D′(2![]() ,﹣1),
,﹣1),
∴直线D′E′的解析式为![]() ,直线BC的解析式为y=
,直线BC的解析式为y=![]() x﹣3,
x﹣3,
由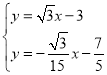 ,解得
,解得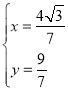 ,,
,,
∴F![]() .
.
把点F向上平移3个单位,向右平移![]() 个单位得到点G,
个单位得到点G,
∴G(![]() ).
).
(3)以点A为圆心,以AE为半径作⊙A,则DE为⊙A的切线.
①如图1中,当CM=CN时,在AE上取一点P,使得AP=PN.设EN=x.
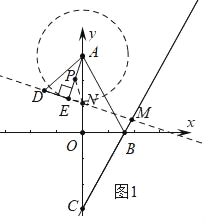
∵CM=CN,∠MCN=30°,
∴∠CNM=∠CMN=75°,
∴∠ANE=∠CNM=75°,
∴∠EAN=15°,
∴∠PAN=∠ANP=15°,
∴∠EPN=30°,
∴PN=AP=2x,PE=![]() x,
x,
∴2x+![]() x=
x=![]() ,
,
∴x=2![]() ﹣3,
﹣3,
∴AN=![]() ,
,
∴CM=CN=![]() =
=![]() .
.
②如图2中,当MN=MC时,作BP⊥MN于P,则四边形ADPB是矩形,PB=AE=![]() ,
,
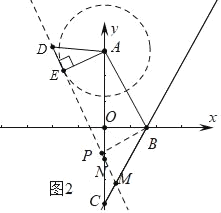
在Rt△PBM中,∠PBM=30°,
∴BM=2,
∴CM=BC﹣BM=2![]() ﹣2.
﹣2.
③如图2﹣1中.CM=CN时,同法可得CM=![]() .
.
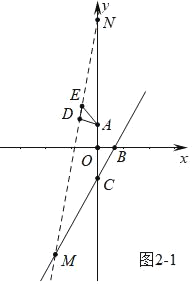
④如图3中,当NC=MN时,D与N重合,作DP⊥BC于P.
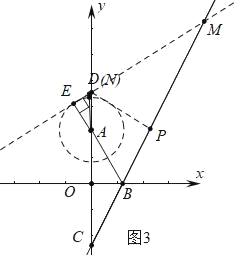
∵CD=6+2=8,∠DCP=30°,
∴PC=PM=4![]() ,
,
∴CM=8![]()
综上所述,满足条件的CM的值为![]() 或
或![]() 或2
或2![]() ﹣2或8
﹣2或8![]() .
.


科目:初中数学 来源: 题型:
【题目】定义:若以一条线段为对角线作正方形,则称该正方形为这条线段的“对角线正方形”.例如,图①中正方形ABCD即为线段BD的“对角线正方形”.如图②,在△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点C出发,沿折线CA﹣AB以5cm/s的速度运动,当点P与点B不重合时,作线段PB的“对角线正方形”,设点P的运动时间为t(s),线段PB的“对角线正方形”的面积为S(cm2).
(1)如图③,借助虚线的小正方形网格,画出线段AB的“对角线正方形”.
(2)当线段PB的“对角线正方形”有两边同时落在△ABC的边上时,求t的值.
(3)当点P沿折线CA﹣AB运动时,求S与t之间的函数关系式.
(4)在整个运动过程中,当线段PB的“对角线正方形”至少有一个顶点落在∠A的平分线上时,直接写出t的值.



查看答案和解析>>
科目:初中数学 来源: 题型:
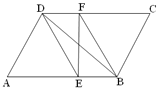
【题目】已知:如图,在□ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=600,AE=2EB,AD=4,求四边形DEBF的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:x为实数,[x]表示不超过x的最大整数,如[3.14]=3,[1]=1,[﹣1.2]=﹣2.请你在学习,理解上述定义的基础上,解决下列问题:设函数y=x﹣[x].
(1)当x=2.15时,求y=x﹣[x]的值;
(2)当0<x<2时,求函数y=x﹣[x]的表达式,并画出函数图象;
(3)当﹣2<x<2时,平面直角坐标系xOy中,以O为圆心,r为半径作圆,且r≤2,该圆与函数y=x﹣[x]恰有一个公共点,请直接写出r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止),此时的俯角为30°.为了便于观察,飞机继续向前飞行了800m到达B点,此时测得点F的俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A,B,C在同一直线上),竖直高度CF约为多少米?(结果保留整数.参考数据:![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与x轴交于A、B两点,与y轴交于点C.直线
与x轴交于A、B两点,与y轴交于点C.直线![]() 经过抛物线与坐标轴的两个交点B和C。
经过抛物线与坐标轴的两个交点B和C。
(1)求直线BC的解析式;
(2)点D是线段BC上的一个动点(与两个端点均不重合),过点D引y轴的平行线PD交抛物线于点P,设抛物线的对称轴为直线![]() ,如果以点P为圆心的⊙P与直线BC相切,请用点P的横坐标x表示⊙P的半径R。
,如果以点P为圆心的⊙P与直线BC相切,请用点P的横坐标x表示⊙P的半径R。
(3)在(2)的基础上判断⊙P与直线![]() 的位置关系。
的位置关系。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)在综合实践课上,同学们以“图形的平移”为主题开展数学活动,如图①,先将一张长为4,宽为3的矩形纸片沿对角线剪开,拼成如图所示的四边形![]() ,
,![]() ,
,![]() ,则拼得的四边形
,则拼得的四边形![]() 的周长是_____.
的周长是_____.

(操作发现)将图①中的![]() 沿着射线
沿着射线![]() 方向平移,连结
方向平移,连结![]() 、
、![]() 、
、![]() 、
、![]() ,如图②.当
,如图②.当![]() 的平移距离是
的平移距离是![]() 的长度时,求四边形
的长度时,求四边形![]() 的周长.
的周长.
(操作探究)将图②中的![]() 继续沿着射线
继续沿着射线![]() 方向平移,其它条件不变,当四边形
方向平移,其它条件不变,当四边形![]() 是菱形时,将四边形
是菱形时,将四边形![]() 沿对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
沿对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
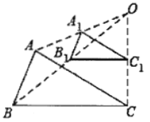
【题目】如图,在![]() 所在平面上任意取一点O(与A、B、C不重合),连接OA、OB、OC,分别取OA、OB、OC的中点
所在平面上任意取一点O(与A、B、C不重合),连接OA、OB、OC,分别取OA、OB、OC的中点![]() 、
、![]() 、
、![]() ,再连接
,再连接![]() 、
、![]() 、
、![]() 得到
得到![]() ,则下列说法不正确的是( )
,则下列说法不正确的是( )
A.![]() 与
与![]() 是位似图形
是位似图形
B.![]() 与是
与是![]() 相似图形
相似图形
C.![]() 与
与![]() 的周长比为2:1
的周长比为2:1
D.![]() 与
与![]() 的面积比为2:1
的面积比为2:1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG.

(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com