
【题目】已知:x为实数,[x]表示不超过x的最大整数,如[3.14]=3,[1]=1,[﹣1.2]=﹣2.请你在学习,理解上述定义的基础上,解决下列问题:设函数y=x﹣[x].
(1)当x=2.15时,求y=x﹣[x]的值;
(2)当0<x<2时,求函数y=x﹣[x]的表达式,并画出函数图象;
(3)当﹣2<x<2时,平面直角坐标系xOy中,以O为圆心,r为半径作圆,且r≤2,该圆与函数y=x﹣[x]恰有一个公共点,请直接写出r的取值范围.
【答案】(1)0.15;(2)①y=x,②当1y=x﹣1, (3)r的取值范围是:0<r<![]() 或x=
或x=![]() .
.
【解析】试题分析:(1)根据[x]的定义进行计算即可;
(2)由已知条件:0<x<1,1≤x<2进行分类讨论,由此可求出结论;
(3)把自变题x在-2<x<2内分四种情况得出相应的函数关系式,并画出图形,确定r的取值即可.
试题解析:解:(1)当x=2.15时,y=x﹣[x]=2.15﹣[2.15]=2.15﹣2=0.15;
(2)①当0<x<1时,[x]=0.∵y=x﹣[x],∴y=x;
②当1≤x<2时,[x]=1
∵y=x﹣[x],∴y=x﹣1;

(3)函数y=x﹣[x](﹣2<x<2),如图,OA=![]() .
.
①当﹣2<x<﹣1,[x]=﹣2,y=x﹣[x]=x+2,②当﹣1≤x<0时,[x]=﹣1,y=x﹣[x]=x+1,③当0≤x<1时,[x]=0,y=x﹣[x ]=x,④当1≤x<2时,[x]=1,y=x﹣[x]=x﹣1,当r=OA= ![]() 时,⊙O与直线y=x﹣1相交于一点,OC=
时,⊙O与直线y=x﹣1相交于一点,OC= ![]() OA=
OA=![]() ,当0<r<
,当0<r<![]() 时,⊙O总与直线y=x相交于一点;
时,⊙O总与直线y=x相交于一点;
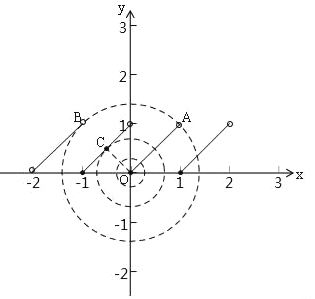
综上所述:r的取值范围是:0<r<![]() 或x=
或x= ![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)图(1)是一个长为2m,宽为2n的矩形,把此矩形沿图中虚线用剪刀均分为四个小长方形,然后按图(2)的形状拼成一个大正方形.请问:这两个图形的什么量不变?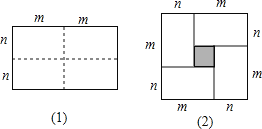
(2)把所得的大正方形面积比原矩形的面积多出的阴影部分的面积用含m,n的代数式表示为(m-n)2或m2-2mn+n2 .
(3)由前面的探索可得出的结论是:在周长一定的矩形中,当 时,面积最大.
(4)若矩形的周长为24cm,则当边长为多少时,该图形的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
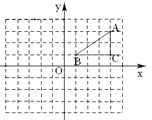
【题目】如图,网格中的每个小正方形的边长均为1个单位长度,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A(4,3),点B(1,1),点C(4,1).
(1)画出Rt△ABC关于y轴对称的Rt△A1B1C1,(点A、B、C的对称点分别是A1、B1、C1),直接写出A1的坐标;
(2)将Rt△ABC向下平移4个单位,得到Rt△A2B2C2(点A、B、C的对应点分别是A2、B2、C2),画出Rt△A2B2C2 ,连接A1C2,直接写出线段A1C2的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm. sin75°≈0.97,cos75°≈0.26,![]() ≈1.73
≈1.73
(1)求该台灯照亮水平桌面的宽度BC.
(2)人在此台灯下看书,将其侧面抽象成如图2所示的几何图形,若书与水平桌面的夹角∠EFC为60°,书的长度EF为24cm,点P为眼睛所在位置,当点P在EF 的垂直平分线上,且到EF距离约为34cm(人的正确看书姿势是眼睛离书距离约1尺≈34cm)时,称点P为“最佳视点”.请通过计算说明最佳视点P在不在灯光照射范围内?
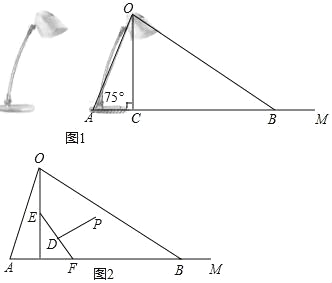
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,用下图的三角形解释二项和的乘方规律.杨辉在注释中提到,在他之前北宋数学家贾宪(1050年左右)也用过上述方法,因此我们称这个三角形为“杨辉三角”或“贾宪三角”.杨辉三角两腰上的数都是![]() ,其余每一个数为它上方(左右)两数的和.事实上,这个三角形给出了
,其余每一个数为它上方(左右)两数的和.事实上,这个三角形给出了![]()
![]() 的展开式(按
的展开式(按![]() 的次数由大到小的顺序)的系数规律.例如,此三角形中第三行的
的次数由大到小的顺序)的系数规律.例如,此三角形中第三行的![]() 个数
个数![]() ,恰好对应着
,恰好对应着![]() 展开式中的各项系数,第四行的
展开式中的各项系数,第四行的![]() 个数
个数![]() ,恰好对应着
,恰好对应着![]() 展开式中的各项系数,等等.请依据上面介绍的数学知识,解决下列问题:
展开式中的各项系数,等等.请依据上面介绍的数学知识,解决下列问题:
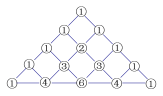
(1)写出![]() 的展开式;
的展开式;
(2)利用整式的乘法验证你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,当0<x≤5时,y= ; 当5<x≤30时,y= ;(直接填最后结果)
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润25万元,那么月需售出多少辆汽车?(注:销售利润=销售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+3与x轴相交于点B,与y轴相交于点A,点E为线段AB中点,∠ABO的平分线BD与y轴相较于点D,点A、C关于点O对称.
x+3与x轴相交于点B,与y轴相交于点A,点E为线段AB中点,∠ABO的平分线BD与y轴相较于点D,点A、C关于点O对称.
(1)求线段DE的长;
(2)一个动点P从点D出发,沿适当的路径运动到直线BC上的点F,再沿射线CB方向移动2![]() 个单位到点G,最后从点G沿适当的路径运动到点E处,当P的运动路径最短时,求此时点G的坐标;
个单位到点G,最后从点G沿适当的路径运动到点E处,当P的运动路径最短时,求此时点G的坐标;
(3)将△ADE绕点A顺时针方向旋转,旋转角度α(0<α≤180°),在旋转过程中DE所在的直线分别与直线BC、直线AC相交于点M、点N,是否存在某一时刻使△CMN为等腰三角形,若存在,请求出CM的长,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,![]() ,
,![]() .点G,E分别在边AB,CD上,点F,H在对角线AC上.若四边形EFGH是菱形,则AG的长是( )
.点G,E分别在边AB,CD上,点F,H在对角线AC上.若四边形EFGH是菱形,则AG的长是( )

A.![]() B.5C.
B.5C.![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)计划购买这两种商品共50件,且投入的经费不超过3200元,那么,最多可购买多少件甲种商品?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com