练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某销售公司5月份销售某种型号汽车，当月该型号汽车的进价为30万元/辆，若当月销售量超过5辆时，每多售出1辆，所有售出的汽车进价均降低0.1万元/辆．根据市场调查，月销售量不会突破30台．

    （1）设当月该型号汽车的销售量为x辆（x≤30，且x为正整数），实际进价为y万元/辆，当0＜x≤5时,y= ; 当5＜x≤30时，y= ;(直接填最后结果)

    （2）已知该型号汽车的销售价为32万元/辆，公司计划当月销售利润25万元，那么月需售出多少辆汽车？（注：销售利润=销售价﹣进价）

    【答案】（1）30，﹣0.1x+30.5．（2）该月需售出10辆汽车．

    【解析】试题分析：（1）根据题意可以得出与的关系．
    （2）根据销售利润=销售价-进价，分类讨论即可．

    试题解析：(1)当且x为整数时，y=30，

    当时,且x为整数时,y=30(x5)×0.1=0.1x+30.5，

    故

    (2)当时,(3230)×5=10<25，不合题意，

    当时,[32(0.1x+30.5)]x=25，

    解得 (舍弃).

    答月需售出10辆汽车.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】甲、乙两辆汽车分别从A、B两地同时出发，沿同一条公路相向而行，乙车出发2h后休息，与甲车相遇后，继续行驶．设甲、乙两车与B地的路程分别为y甲（km），y乙（km），甲车行驶的时间为x（h），y甲、y乙与x之间的函数图象如图所示，结合图象解答下列问题：

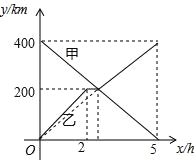
    （1）乙车休息了 h．

    （2）求乙车与甲车相遇后y乙关于x的函数表达式，并写出自变量x的取值范围．

    （3）当两车相距40km时，求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，，，满足，，则__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以点P（-1,0）为圆心的圆，交x轴于B、C两点（B在C的左侧），交y轴于A、D两点（A在D的下方），AD=，将△ABC绕点P旋转180°，得到△MCB．

    （1）求B、C两点的坐标；

    （2）请在图中画出线段MB、MC，并判断四边形ACMB的形状（不必证明），求出点M的坐标；

    （3）动直线l从与BM重合的位置开始绕点B顺时针旋转，到与BC重合时停止，设直线l与CM交点为E，点Q为BE的中点，过点E作EG⊥BC于G，连接MQ、QG．请问在旋转过程中∠MQG的大小是否变化？若不变，求出∠MQG的度数；若变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：x为实数，[x]表示不超过x的最大整数，如[3.14]=3，[1]=1，[﹣1.2]=﹣2．请你在学习，理解上述定义的基础上，解决下列问题：设函数y=x﹣[x]．

    （1）当x=2.15时，求y=x﹣[x]的值；

    （2）当0＜x＜2时，求函数y=x﹣[x]的表达式，并画出函数图象；

    （3）当﹣2＜x＜2时，平面直角坐标系xOy中，以O为圆心，r为半径作圆，且r≤2，该圆与函数y=x﹣[x]恰有一个公共点，请直接写出r的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，菱形的顶点与原点重合，点在轴的正半轴上，点在函数的图象上，点的坐标为.

    (1)求的值.

    (2)将点沿轴正方向平移得到点，当点在函数的图象上时，求的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线与x轴交于A、B两点，与y轴交于点C.直线经过抛物线与坐标轴的两个交点B和C。

    （1）求直线BC的解析式；

    （2）点D是线段BC上的一个动点（与两个端点均不重合），过点D引y轴的平行线PD交抛物线于点P，设抛物线的对称轴为直线，如果以点P为圆心的⊙P与直线BC相切，请用点P的横坐标x表示⊙P的半径R。

    （3）在（2）的基础上判断⊙P与直线的位置关系。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把四张形状大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面为长方形（长为3a厘米，宽为（2a－b）厘米）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示．

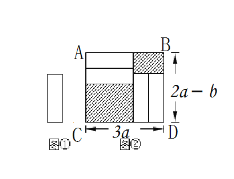
    （1）求大长方形ABCD的周长；

    （2）求图②中两块阴影部分周长之和．（用含a，b的式子表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)根据下面给出的数轴，解答下面的问题：

    ①请你根据图中A、B两点的位置，分别写出它们所表示的有理数A：______，B：______；

    ②观察数轴，与点A的距离为4的点表示的数是：______；

    ③若将数轴折叠，使得A点与-3表示的点重合，则B点与数______表示的点重合．

    (2)如图，数轴上A，B两点对应的有理数分别为10和15，点P从点A出发，以每秒1个单位长度的速度沿数轴正方向运动，点Q同时从原点O出发，以每秒2个单位长度的速度沿数轴正方向运动，设运动时间为t秒．

    ①当0＜t＜5，用含t的式子填空：BP＝______，AQ＝______；

    ②当t＝2时，求PQ的值；

    查看答案和解析>>

    同步练习册答案