
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() 满足
满足![]() ,
,![]() ,则
,则![]() __________.
__________.
【答案】60
【解析】
先利用单项式乘以多项式法则将要求值的多项式进行整理,将题目所给的有确定值的式子进行变形,得出所需要的式子的值,运用整体代入法既可求解.
∵m+n=p+q=4
∴(m+n)(p+q)=4×4=16
∵(m+n)(p+q)=mp+mq+np+nq
∴mp+mq+np+nq=16
∵mp+nq=6
∴mq+np=10
∴(m2+n2)pq+mn(p2+q2)
=m2pq+n2pq+mnp2+mnq2
=mpmq+npnq+mpnp+nqmq
=mpmq+mpnp+npnq+nqmq
=mp(mq+np)+np(nq+mq)
=(mp+nq)(np+mq)
=6×10
=60
故答案为:60


科目:初中数学 来源: 题型:
【题目】如图,用三种大小不同的五个正方形和一个缺角的长方形拼成长方形 ABCD,其中,NH=NG 1cm ,设 BF acm .
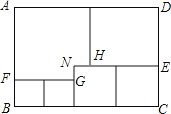
(1)用含 a 的代数式分别表示 CE,DE;
(2)求长方形 ABCD 的周长.(用含 a 的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读计算:
阅读下列各式:![]() ,
,![]() ,
,![]() ……
……
回答下列三个问题:
(1)验证:(5×0.2)10=__________;510×0.210=__________.
(2)通过上述验证,归纳得出:![]() =__________;
=__________;![]() =__________.
=__________.
(3)请应用上述性质计算:
①![]()
②![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
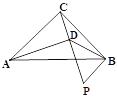
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,P为Rt△ABC外一点,且∠BPC=60°,过点A作AD⊥PC交PC于点D,连接BD,若∠PDB=45°,BD=![]() ,则PC= _____.
,则PC= _____.
查看答案和解析>>
科目:初中数学 来源: 题型:
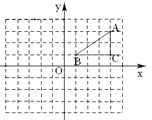
【题目】如图,网格中的每个小正方形的边长均为1个单位长度,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A(4,3),点B(1,1),点C(4,1).
(1)画出Rt△ABC关于y轴对称的Rt△A1B1C1,(点A、B、C的对称点分别是A1、B1、C1),直接写出A1的坐标;
(2)将Rt△ABC向下平移4个单位,得到Rt△A2B2C2(点A、B、C的对应点分别是A2、B2、C2),画出Rt△A2B2C2 ,连接A1C2,直接写出线段A1C2的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
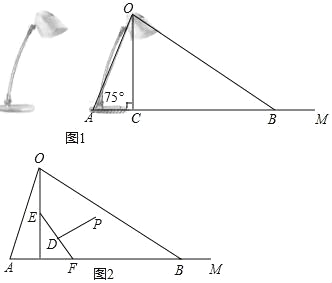
【题目】如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm. sin75°≈0.97,cos75°≈0.26,![]() ≈1.73
≈1.73
(1)求该台灯照亮水平桌面的宽度BC.
(2)人在此台灯下看书,将其侧面抽象成如图2所示的几何图形,若书与水平桌面的夹角∠EFC为60°,书的长度EF为24cm,点P为眼睛所在位置,当点P在EF 的垂直平分线上,且到EF距离约为34cm(人的正确看书姿势是眼睛离书距离约1尺≈34cm)时,称点P为“最佳视点”.请通过计算说明最佳视点P在不在灯光照射范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,当0<x≤5时,y= ; 当5<x≤30时,y= ;(直接填最后结果)
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润25万元,那么月需售出多少辆汽车?(注:销售利润=销售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EF与AB,CD分别交于点G,H,∠CHG的平分线HM交AB于点M,若∠EGB=50°,则∠GMH的度数为( )

A. 50°B. 55°C. 60°D. 65°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com