
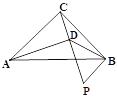
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,P为Rt△ABC外一点,且∠BPC=60°,过点A作AD⊥PC交PC于点D,连接BD,若∠PDB=45°,BD=![]() ,则PC= _____.
,则PC= _____.
科目:初中数学 来源: 题型:
【题目】小明为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)
(1)求小明此时与地面的垂直距离CD的值;
(2)小明的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(sin15°≈0.2588,cos15°≈0.9659 ,tan≈.0.2677 )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:
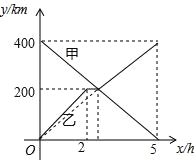
(1)乙车休息了 h.
(2)求乙车与甲车相遇后y乙关于x的函数表达式,并写出自变量x的取值范围.
(3)当两车相距40km时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据语句画图,并回答问题,如图,∠AOB内有一点P.
(1)过点P画PC∥OB交OA于点C,画PD∥OA交OB于点D.
(2)写出图中与∠CPD互补的角 .(写两个即可)
(3)写出图中∠O相等的角 .(写两个即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】又到一年丰收季,重庆外国语学校“国内中考、高考、国内保送、出国留学”捷报频传.作为准初三的初二年级学生希望抓紧暑期更好的提升自我.张同学采用随机抽样的方式对初二年级学生此次暑期生活的主要计划进行了问卷调查,并将调查结果按照“A社会实践类、B学习提高类、C游艺娱乐类、D其他”进行了分类统计,并绘制了如图1和如图2两幅不完整的统计图.(接受调查的每名同学只能在四类中选择其中一种类型,不可多选或不选.)请根据图中提供的信息完成以下问题.
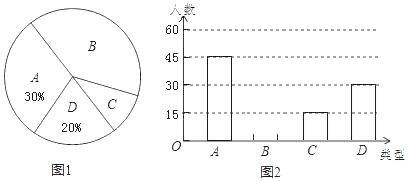
(1)扇形统计图中表示B类的扇形的圆心角是 度,并补全条形统计图;
(2)张同学已从被调查的同学中确定了甲、乙、丙、丁四名同学进行开学后的经验交流,并计划在这四人中选出两人的宝贵经验刊登在本班班刊上.请利用画树状图或列表的方法求出甲同学的经验刊登在班刊上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )
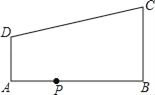
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=![]() ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.

(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为3a厘米,宽为(2a-b)厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.
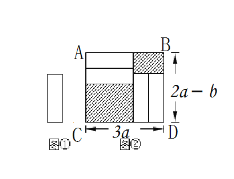
(1)求大长方形ABCD的周长;
(2)求图②中两块阴影部分周长之和.(用含a,b的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com