
【题目】小明为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)
(1)求小明此时与地面的垂直距离CD的值;
(2)小明的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(sin15°≈0.2588,cos15°≈0.9659 ,tan≈.0.2677 )

【答案】(1)小华与地面的垂直距离CD的值是5.2m; (2)楼房AB的高度是26.1m.
【解析】试题分析:(1)sin15°=![]() ,CD= BD·sin15°,将已知数值代入计算即可;(2)AB=AF+BF,BF=CD+ED不难求得,因为∠AEF=45°,所以AF=EF=BC,要求BC利用cos15°=
,CD= BD·sin15°,将已知数值代入计算即可;(2)AB=AF+BF,BF=CD+ED不难求得,因为∠AEF=45°,所以AF=EF=BC,要求BC利用cos15°=![]() ,即BC=BD·cos15°.
,即BC=BD·cos15°.
试题解析:
(1)在Rt△BCD中,∠CBD=15°,BD=20,
∴CD=BD·sin15°,
∴CD=5.2(m),
答:小华与地面的垂直距离CD的值是5.2m;
(2)在Rt△AFE中,
∵∠AEF=45°,
∴AF=EF=BC,
BC=BD·cos15°≈19.3(m),
∴AB=AF+DE+CD=19.3+1.6+5.2=26.1(m).
答:楼房AB的高度是26.1m.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
售价(元/盏) | 60 | 100 |
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
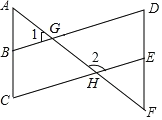
【题目】如图,已知AF分别与BD、CE交于点G、H,其中∠1+∠2=180°.
(1)判断BD和CE有怎样的位置关系,并说明理由;
(2)若∠A=∠F,探索∠C与∠D的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
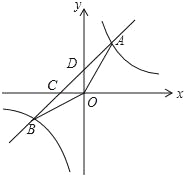
【题目】如图,点A(m,4),B(﹣4,n)在反比例函数y=![]() (k>0)的图象上,经过点A、B的直线与x轴相交于点C,与y轴相交于点D.
(k>0)的图象上,经过点A、B的直线与x轴相交于点C,与y轴相交于点D.
(1)若m=2,求n的值;
(2)求m+n的值;
(3)连接OA、OB,若tan∠AOD+tan∠BOC=1,求直线AB的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面说法正确的是( ).
A. 检测一批进口食品的质量应采用全面调查
B. 从![]() 万名考生的成绩中抽取
万名考生的成绩中抽取![]() 名考生的成绩作为样本,样本容量是
名考生的成绩作为样本,样本容量是![]() 万
万
C. 反应你本学年数学成绩的变化情况宜采用扇形统计图
D. 一组数据的样本容量是![]() ,最大值是
,最大值是![]() ,最小值是
,最小值是![]() ,取组距为
,取组距为![]() ,可分为
,可分为![]() 组
组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=![]() ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com