
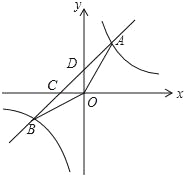
【题目】如图,点A(m,4),B(﹣4,n)在反比例函数y=![]() (k>0)的图象上,经过点A、B的直线与x轴相交于点C,与y轴相交于点D.
(k>0)的图象上,经过点A、B的直线与x轴相交于点C,与y轴相交于点D.
(1)若m=2,求n的值;
(2)求m+n的值;
(3)连接OA、OB,若tan∠AOD+tan∠BOC=1,求直线AB的函数关系式.
【答案】(1)n=﹣2;(2)m+n=0;(3)y=x+2
【解析】试题分析:(1)先把A点坐标代入y=![]() 求出k的值得到反比例函数解析式为y=
求出k的值得到反比例函数解析式为y=![]() ,然后把B(﹣4,n)代入y=
,然后把B(﹣4,n)代入y=![]() 可求出n的值;(2)利用反比例函数图象上点的坐标特征得到4m=k,﹣4n=k,然后把两式相减消去k即可得到m+n的值;(3)作AE⊥y轴于E,BF⊥x轴于F,如图,利用正切的定义得到tan∠AOE=
可求出n的值;(2)利用反比例函数图象上点的坐标特征得到4m=k,﹣4n=k,然后把两式相减消去k即可得到m+n的值;(3)作AE⊥y轴于E,BF⊥x轴于F,如图,利用正切的定义得到tan∠AOE=![]() =
=![]() ,tan∠BOF=
,tan∠BOF=![]() =
=![]() ,则
,则![]() +
+![]() =1,加上m+n=0,于是可解得m=2,n=﹣2,从而得到A(2,4),B(﹣4,﹣2),然后利用待定系数法求直线AB的解析式.
=1,加上m+n=0,于是可解得m=2,n=﹣2,从而得到A(2,4),B(﹣4,﹣2),然后利用待定系数法求直线AB的解析式.
试题解析:(1)当m=2,则A(2,4),
把A(2,4)代入y=![]() 得k=2×4=8,
得k=2×4=8,
所以反比例函数解析式为y=![]() ,
,
把B(﹣4,n)代入y=![]() 得﹣4n=8,解得n=﹣2;
得﹣4n=8,解得n=﹣2;
(2)因为点A(m,4),B(﹣4,n)在反比例函数y=![]() (k>0)的图象上,
(k>0)的图象上,
所以4m=k,﹣4n=k,
所以4m+4n=0,即m+n=0;
(3)作AE⊥y轴于E,BF⊥x轴于F,如图,
在Rt△AOE中,tan∠AOE=![]() =
=![]() ,
,
在Rt△BOF中,tan∠BOF=![]() =
=![]() ,
,
而tan∠AOD+tan∠BOC=1,
所以![]() +
+![]() =1,
=1,
而m+n=0,解得m=2,n=﹣2,
则A(2,4),B(﹣4,﹣2),
设直线AB的解析式为y=px+q,
把A(2,4),B(﹣4,﹣2)代入得![]() ,解得
,解得![]() ,
,
所以直线AB的解析式为y=x+2.


科目:初中数学 来源: 题型:
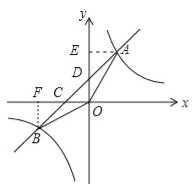
【题目】如图,在平面直角坐标系中,一次函数y=2x-5的图象经过正方形OABC的顶点A和C,则正方形OABC的面积为( )

A.9B.10C.12D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”,这个三角形给出了(a+b)n (n=1,2,3,4,…)的展开式的系数规律(按n的次数由大到小的顺序):
1 1 (a+b)1=a+b
1 2 1 (a+b)2=a2+2ab+b2
1 3 3 1 (a+b)3=a3+3a2b+3ab2+b3
1 4 6 4 1 (a+b)4=a4+4a3b+6a2b2+4ab3+b4
…… ……
请依据上述规律,写出(x1)2019展开式中含x2018项的系数是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)
(1)求小明此时与地面的垂直距离CD的值;
(2)小明的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(sin15°≈0.2588,cos15°≈0.9659 ,tan≈.0.2677 )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,点P是∠AOB内的定点,且OP=3.若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )

A.12B.9C.6D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,同学们探究了角平分线的作法.下面给出三个同学的作法:
小红的作法
如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,再过点O作MN的垂线,垂足为P,则射线OP便是∠AOB的平分线.

小明的作法 如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线.
|
小刚的作法 如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,则射线OP便是∠AOB的平分线.
|
请根据以上情境,解决下列问题
(1)小红的作法依据是 .
(2)为说明小明作法是正确的,请帮助他完成证明过程.
证明:∵OM=ON,OC=OC, ,
∴△OMC≌△ONC( )(填推理的依据)
(3)小刚的作法正确吗?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于
的图像相交于![]() 、
、![]() 两点.
两点.

(1)求出两函数解析式;
(2)根据图像回答:当![]() 为何值时,一次函数的函数值大于反比例函数的函数值?
为何值时,一次函数的函数值大于反比例函数的函数值?
(3)连接![]() 、
、![]() ,试求
,试求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
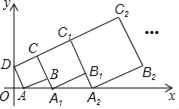
【题目】在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式![]() .
.
解∵![]() ,∴
,∴![]() 可化为
可化为![]() .
.
由有理数的乘法法则:两数相乘,同号得正,得:①![]() ②
②![]()
解不等式组①,得![]() ,解不等式组②,得
,解不等式组②,得![]()
∴![]() 的解集为
的解集为![]() 或
或![]() .
.
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(1)一元二次不等式![]() 的解集为____________;
的解集为____________;
(2)试解一元二次不等式![]() ;
;
(3)试解不等式![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com