
����Ŀ����ѧ����ϣ�ͬѧ��̽���˽�ƽ���ߵ������������������ͬѧ��������
�������
��ͼ����AOB��һ������ǣ��ڱ�OA��OB�Ϸֱ�ȡOM��ON���ٹ���O��MN�Ĵ��ߣ�����ΪP��������OP���ǡ�AOB��ƽ���ߣ�

С�������� ��ͼ����AOB��һ������ǣ��ڱ�OA��OB�Ϸֱ�ȡOM=ON���ƶ��dzߣ�ʹ�dz�������ͬ�Ŀ̶ȷֱ���M��N�غϣ����dz߶���C������OC���ǡ�AOB��ƽ���ߣ�
|
С�յ����� ��ͼ����AOB��һ������ǣ��ڱ�OA��OB�Ϸֱ�ȡOM��ON���ٷֱ����M��N��OA��OB�Ĵ��ߣ�����ΪP��������OP���ǡ�AOB��ƽ���ߣ�
|
����������龳�������������
(1)������������� ��
(2)Ϊ˵��С����������ȷ�ģ�����������֤�����̣�
֤������OM��ON��OC��OC�� ��
���OMC�ա�ONC( )(������������)
(3)С�յ�������ȷ��?��˵������
���𰸡���1���������������ߺ�һ��������2��CM=CN���߱߱ߣ���3����ȷ��֤������⣮
��������
��1�����õ������������ߺ�һ���������ɵõ����۳�����
��2������SSS������֤����OMC�ա�ONC����ȫ�������ɣ�
��3������HL������֤��Rt��OPM��Rt��OPN�����ɵõ����۳�����
�⣺��1����OM=ON��
���OMN�ǵ��������Σ�
��OP��MN��
��OP�ǵױ��ϵĸߣ�Ҳ�ǵױ��ϵ����ߣ�Ҳ�ǡ�MON�Ľ�ƽ���ߣ�
�ʴ�Ϊ���������������ߺ�һ������
��2��֤������OM��ON��OC��OC��CM=CN��
���OMC�ա�ONC���߱߱ߣ���
���MOC=��NOC��
��OCƽ�֡�AOB��
�ʴ�Ϊ��CM=CN���߱߱ߣ�
��3��С�յ�������ȷ��֤�����£�
��PM��OA��PN��OB��
���OMP=��ONP=90�㣬
��OM=ON��OP=OP��
��Rt��OPM��Rt��OPN��HL����
���MOP=��NOP��
��OPƽ�֡�AOB��
![]() С�յ�������ȷ��
С�յ�������ȷ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�˳а���һ��������,�������һ���������.���������ϳ����Ķ��Ӱ�æ.�������������������������������60����,��ÿ���㶼���ϱ��,�Ż�����;����2��,���������״������ڴ�������50����,���������2������ǵ�.���赱ʱ������������Ϊ2.8Ԫ/��,ƽ��ÿ�������2.3��,���ܰ���������һ�½�������������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
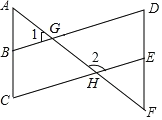
����Ŀ����ͼ����֪AF�ֱ���BD��CE���ڵ�G��H�����С�1����2=180��.
��1���ж�BD��CE��������λ�ù�ϵ����˵�����ɣ�
��2������A=��F��̽����C���D��������ϵ����֤����Ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC����ֱ������ϵ�ڣ����С�CAB��90�㣬BC��5����A��B������ֱ�Ϊ(1��0)��(4��0)������ABC��x������ƽ�ƣ�����C����ֱ��y��2x��6��ʱ���߶�BCɨ�������Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
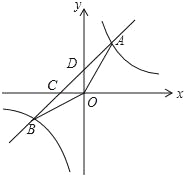
����Ŀ����ͼ����A��m��4����B����4��n���ڷ���������y=![]() ��k��0����ͼ���ϣ�������A��B��ֱ����x���ཻ�ڵ�C����y���ཻ�ڵ�D��
��k��0����ͼ���ϣ�������A��B��ֱ����x���ཻ�ڵ�C����y���ཻ�ڵ�D��
��1����m=2����n��ֵ��
��2����m+n��ֵ��
��3������OA��OB����tan��AOD+tan��BOC=1����ֱ��AB�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ǵ�һ�����ڵĵ㣬ֱ��
�ǵ�һ�����ڵĵ㣬ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() �Ḻ�����ڵ�
�Ḻ�����ڵ�![]() ������
������![]() ��
��![]() ��
��

��1����![]() �������
�������
��2�����![]() �������
�������![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��.
A. ���һ������ʳƷ������Ӧ����ȫ�����
B. ��![]() ���������ijɼ��г�ȡ
���������ijɼ��г�ȡ![]() �������ijɼ���Ϊ����������������
�������ijɼ���Ϊ����������������![]() ��
��
C. ��Ӧ�㱾ѧ����ѧ�ɼ��ı仯����˲�������ͳ��ͼ
D. һ�����ݵ�����������![]() �����ֵ��
�����ֵ��![]() ����Сֵ��
����Сֵ��![]() ��ȡ���Ϊ
��ȡ���Ϊ![]() ���ɷ�Ϊ
���ɷ�Ϊ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���֪��![]() ����
����![]() ��������ת�任�������εõ�
��������ת�任�������εõ�![]() ��
��![]() ��ֱ�Ƕ��������Ϊ�� ��
��ֱ�Ƕ��������Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com