
【题目】若等腰三角形的两边长为![]() 和
和![]() ,则它腰上的高长度为______.
,则它腰上的高长度为______.
【答案】![]()
【解析】
先由三角形三边的关系判断出等腰三角形的三边长分别为8,8,4,再分别作出底边和腰上的高线,由勾股定理求出底边上的高,再由三角形等积式及可求解.
情况1:当等腰三角形的腰长为4时,则这个等腰三角形的三边长分别为4、4、8,
∵4+4=8,不满足三角形的三边关系,
∴此情况不存在等腰三角形;
情况2:当等腰三角形的腰长为8时,则这个等腰三角形的三边长分别为4、8、8,
∵4+8>8,8-4<8,符合三角形的三边关系,
∴此情况存在等腰三角形,
综上所述,这个等腰三角形的腰长为8,底边长为4.
如图,
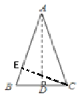
AB=AC=8,BC=4,过点A作AD![]() BC于点D,
BC于点D,
∵AB=AC=8,AD⊥ BC,BC=8
∴BD=![]() BC=2(等腰三角形的三线合一)
BC=2(等腰三角形的三线合一)
由勾股定理得:AD=![]() ,
,
过点C作CE![]() AB于点E,
AB于点E,
由![]() ,得
,得![]() ,
,
即腰上的高为![]() .
.


科目:初中数学 来源: 题型:
【题目】数学活动课上,同学们探究了角平分线的作法.下面给出三个同学的作法:
小红的作法
如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,再过点O作MN的垂线,垂足为P,则射线OP便是∠AOB的平分线.

小明的作法 如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线.
|
小刚的作法 如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,则射线OP便是∠AOB的平分线.
|
请根据以上情境,解决下列问题
(1)小红的作法依据是 .
(2)为说明小明作法是正确的,请帮助他完成证明过程.
证明:∵OM=ON,OC=OC, ,
∴△OMC≌△ONC( )(填推理的依据)
(3)小刚的作法正确吗?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线y=x的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为
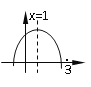
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式![]() .
.
解∵![]() ,∴
,∴![]() 可化为
可化为![]() .
.
由有理数的乘法法则:两数相乘,同号得正,得:①![]() ②
②![]()
解不等式组①,得![]() ,解不等式组②,得
,解不等式组②,得![]()
∴![]() 的解集为
的解集为![]() 或
或![]() .
.
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(1)一元二次不等式![]() 的解集为____________;
的解集为____________;
(2)试解一元二次不等式![]() ;
;
(3)试解不等式![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
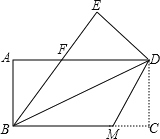
【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线C:y=x2经过变化可得到抛物线C1:y1=a1x(x﹣b1),C1与x轴的正半轴交与点A1,且其对称轴分别交抛物线C,C1于点B1,D1,此时四边形OB1A1D1恰为正方形;按上述类似方法,如图2,抛物线C1:y1=a1x(x﹣b1)经过变换可得到抛物线C2:y2=a2x(x﹣b2),C2与x轴的正半轴交与点A2,且其对称轴分别交抛物线C1,C2于点B2,D2,此时四边形OB2A2D2也恰为正方形;按上述类似方法,如图3,可得到抛物线C3:y3=a3x(x﹣b3)与正方形OB3A3D3.请探究以下问题:
(1)填空:a1= ,b1= ;
(2)求出C2与C3的解析式;
(3)按上述类似方法,可得到抛物线Cn:yn=anx(x﹣bn)与正方形OBnAnDn(n≥1).
①请用含n的代数式直接表示出Cn的解析式;
②当x取任意不为0的实数时,试比较y2015与y2016的函数值的大小并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由正比例函数![]() 沿
沿![]() 轴的正方向平移4个单位而成的一次函数
轴的正方向平移4个单位而成的一次函数![]()
的图像与反比例函数![]() (
(![]() )在第一象限的图像交于A(1,n)和B两点.
)在第一象限的图像交于A(1,n)和B两点.
(1)求一次函数![]() 和反比例函数的解析式;
和反比例函数的解析式;
(2)求△ABO的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“分组合作学习”已成为推动课堂教学改革,打造自主高效课堂的重要措施.某中学从全校学生中随机抽取部分学生对“分组合作学习”实施后的学习兴趣情况进行调查分析,统计图如下:

请结合图中信息解答下列问题:
(1)求出随机抽取调查的学生人数;
(2)补全分组后学生学习兴趣的条形统计图;
(3)分组后学生学习兴趣为“中”的所占的百分比和对应扇形的圆心角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com