
【题目】如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线y=x的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点.

【答案】(1)抛物线解析式为y=x2﹣1;(2)△ABM为直角三角形.理由见解析;(3)当m≤![]() 时,平移后的抛物线总有不动点.
时,平移后的抛物线总有不动点.
【解析】试题分析:(1)分别写出A、B的坐标,利用待定系数法求出抛物线的解析式即可;
根据OA=OM=1,AC=BC=3,分别得到∠MAC=45°,∠BAC=45°,得到∠BAM=90°,进而得到△ABM是直角三角形;
(3)根据抛物线的平以后的顶点设其解析式为![]() ,
,
∵抛物线的不动点是抛物线与直线![]() 的交点,∴
的交点,∴![]() ,
,
方程![]() 总有实数根,则
总有实数根,则![]() ≥0,得到m的取值范围即可
≥0,得到m的取值范围即可
试题解析:解:(1)∵点A是直线![]() 与
与![]() 轴的交点,∴A点为(-1,0)
轴的交点,∴A点为(-1,0)
∵点B在直线![]() 上,且横坐标为2,∴B点为(2,3)
上,且横坐标为2,∴B点为(2,3)
∵过点A、B的抛物线的顶点M在![]() 轴上,故设其解析式为:
轴上,故设其解析式为: ![]()
∴![]() ,解得:
,解得: ![]()
∴抛物线的解析式为![]() .
.
(2)△ABM是直角三角形,且∠BAM=90°.理由如下:
作BC⊥![]() 轴于点C,∵A(-1,0)、B(2,3)∴AC=BC=3,∴∠BAC=45°;
轴于点C,∵A(-1,0)、B(2,3)∴AC=BC=3,∴∠BAC=45°;
点M是抛物线![]() 的顶点,∴M点为(0,-1)∴OA=OM=1,
的顶点,∴M点为(0,-1)∴OA=OM=1,
∵∠AOM=90°∴∠MAC=45°;
∴∠BAM=∠BAC+∠MAC=90°∴△ABM是直角三角形.
(3)将抛物线的顶点平移至点(![]() ,
, ![]() ),则其解析式为
),则其解析式为![]() .
.
∵抛物线的不动点是抛物线与直线![]() 的交点,∴
的交点,∴![]()
化简得: ![]()
∴![]() =
=![]() =
=![]()
当![]() 时,方程
时,方程![]() 总有实数根,即平移后的抛物线总有不动点
总有实数根,即平移后的抛物线总有不动点
∴![]() .
.


科目:初中数学 来源: 题型:
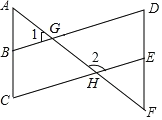
【题目】如图,已知AF分别与BD、CE交于点G、H,其中∠1+∠2=180°.
(1)判断BD和CE有怎样的位置关系,并说明理由;
(2)若∠A=∠F,探索∠C与∠D的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面说法正确的是( ).
A. 检测一批进口食品的质量应采用全面调查
B. 从![]() 万名考生的成绩中抽取
万名考生的成绩中抽取![]() 名考生的成绩作为样本,样本容量是
名考生的成绩作为样本,样本容量是![]() 万
万
C. 反应你本学年数学成绩的变化情况宜采用扇形统计图
D. 一组数据的样本容量是![]() ,最大值是
,最大值是![]() ,最小值是
,最小值是![]() ,取组距为
,取组距为![]() ,可分为
,可分为![]() 组
组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进![]() 种型号的衣服9件,
种型号的衣服9件,![]() 种型号的衣服10件,则共需1810元;若购进
种型号的衣服10件,则共需1810元;若购进![]() 种型号的衣服12件,
种型号的衣服12件,![]() 种型号的衣服,8件,共需1880元;已知销售一种
种型号的衣服,8件,共需1880元;已知销售一种![]() 种型号衣服可获利18元,销售一种
种型号衣服可获利18元,销售一种![]() 种型号衣服可获利30元,要时这次销售获利不少于699元,且
种型号衣服可获利30元,要时这次销售获利不少于699元,且![]() 种型号衣服不多于28件.
种型号衣服不多于28件.
(1)求![]() 型号的衣服进价各是多少元?
型号的衣服进价各是多少元?
(2)已知购进![]() 型号衣服是
型号衣服是![]() 型号衣服的2倍还多4件,则商店这次进货中一共有几种方案.
型号衣服的2倍还多4件,则商店这次进货中一共有几种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题: 同学们,我们把学习新的数学知识的时候,经常利用“化归“的数学思想方法解决问题,比如,我们在学习二元一次方程组的解法时,是通过“消元”的方法将二元方程化归成我们所 熟悉的一元方程,从而正确求解.下面我们就利用“化归”的数学方法解决新的问题. 首先,我们把像这样,只含有一个未知数,并且未知教的最高次数是![]() 的不等式,称为一元二次不等式.通过以前的学习,我们已经认识了一无一次不等式、一元一次不等式组并掌握 了它们的解法.同学们,你们能类比一元一次不等式(组)的解法求出一元二次不等式的解 集吗? 例题:解一元二次不等式
的不等式,称为一元二次不等式.通过以前的学习,我们已经认识了一无一次不等式、一元一次不等式组并掌握 了它们的解法.同学们,你们能类比一元一次不等式(组)的解法求出一元二次不等式的解 集吗? 例题:解一元二次不等式![]() 为了解决这个问题,我们需要将一元二次不等式“化归”到一元一次不等式(组),通过平方差公式的逆用,我们可以把
为了解决这个问题,我们需要将一元二次不等式“化归”到一元一次不等式(组),通过平方差公式的逆用,我们可以把![]() 写成
写成![]() 的形式,从面将
的形式,从面将![]() 转化为
转化为![]() ,然后再利用两数相乘的符号性质将一元二次不等式转化成一元一次不等式(组),从而解决问题.
,然后再利用两数相乘的符号性质将一元二次不等式转化成一元一次不等式(组),从而解决问题.
解:![]()
![]() 可化为
可化为![]()
由有理数的乘法法则“两数相乘,同号得正”,得①![]() ②
②![]()
解不等式组①, ![]()
解不等式组②, ![]()
即一元二次不等式![]() 的解集为
的解集为![]()
拓展应用:
![]() 求一元二次不等式
求一元二次不等式![]() 的解集.
的解集.
![]() 求分式不等式
求分式不等式![]() 的解集.
的解集.
![]() 求一元二次不等式
求一元二次不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=![]() ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() ,边
,边![]() 上有一点
上有一点![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,联结
上,联结![]() ,
,![]() ,联结
,联结![]() ,
,![]() ,
,![]() .
.
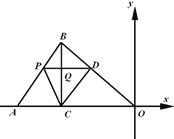
(1)求直线![]() 的解析式及点
的解析式及点![]() 的坐标;
的坐标;
(2当![]() 时,求出点
时,求出点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 在射线
在射线![]() 上,
上,![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com