练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下面说法正确的是（ ）.

    A. 检测一批进口食品的质量应采用全面调查

    B. 从万名考生的成绩中抽取名考生的成绩作为样本，样本容量是万

    C. 反应你本学年数学成绩的变化情况宜采用扇形统计图

    D. 一组数据的样本容量是，最大值是，最小值是，取组距为，可分为组

    【答案】D

    【解析】

    根据全面调查与抽样调查，样本的意义，调查方式的选择，统计图的选择，频数分布表即可进行判断．

    解：A、检测一批进口食品的质量应采用抽样调查，故错误；
    B、从万名考生的成绩中抽取名考生的成绩作为样本，样本容量是300，故错误；
    C、反映你本学年数学成绩的变化情况宜采用折线统计图，故错误；
    D、一组数据的样本容量是，最大值是141，最小值是60，取组距为10，可分为9组，故正确．
    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我们知道平行四边形有很多性质，现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论.

    （发现与证明）中，，将沿翻折至，连结.

    结论1：与重叠部分的图形是等腰三角形；

    结论2：.

    试证明以上结论.

    （应用与探究）

    在中，已知，，将沿翻折至，连结.若以、、、为顶点的四边形是正方形，求的长.（要求画出图形）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明为了测量楼房AB的高度，他从楼底的B处沿着斜坡向上行走20m，到达坡顶D处．已知斜坡的坡角为15°．（以下计算结果精确到0.1m）

    （1）求小明此时与地面的垂直距离CD的值；

    （2）小明的身高ED是1.6m，他站在坡顶看楼顶A处的仰角为45°，求楼房AB的高度．（sin15°≈0.2588，cos15°≈0.9659 ，tan≈.0.2677 )

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学活动课上，同学们探究了角平分线的作法．下面给出三个同学的作法：

    小红的作法

    如图，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，再过点O作MN的垂线，垂足为P，则射线OP便是∠AOB的平分线．

    小明的作法

    如图，∠AOB是一个任意角，在边OA、OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合，过角尺顶点C的射线OC便是∠AOB的平分线．

    小刚的作法

    如图，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，再分别过点M，N作OA，OB的垂线，交点为P，则射线OP便是∠AOB的平分线．

    请根据以上情境，解决下列问题

    (1)小红的作法依据是 ．

    (2)为说明小明作法是正确的，请帮助他完成证明过程．

    证明：∵OM＝ON，OC＝OC， ，

    ∴△OMC≌△ONC( )(填推理的依据)

    (3)小刚的作法正确吗?请说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数的图像与反比例函数的图像相交于、两点．

    （1）求出两函数解析式；

    （2）根据图像回答：当为何值时，一次函数的函数值大于反比例函数的函数值？

    （3）连接、，试求的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，

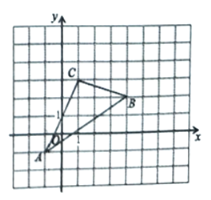
    （1）请直接写出、两点的坐标；

    （2）若把向上平移个单位，再向右平移个单位得，请在图中画出，并写出点的坐标；

    （3）求的面积。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

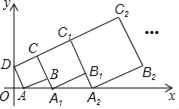
    【题目】在平面直角坐标系中，正方形ABCD的位置如右图所示，点A的坐标为（1，0），点D的坐标为（0，2）．延长CB交x轴于点A1，作正方形A1B1C1C；延长C1B1交x轴于点A2，作正方形A2B2C2C1，…按这样的规律进行下去，第2017个正方形的面积为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点，且点A在x轴上，点B的横坐标为2，连结AM、BM．

    （1）求抛物线的函数关系式；

    （2）判断△ABM的形状，并说明理由；

    （3）把抛物线与直线y=x的交点称为抛物线的不动点．若将（1）中抛物线平移，使其顶点为（m，2m），当m满足什么条件时，平移后的抛物线总有不动点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线C：y=x2经过变化可得到抛物线C1：y1=a1x（x﹣b1），C1与x轴的正半轴交与点A1，且其对称轴分别交抛物线C，C1于点B1，D1，此时四边形OB1A1D1恰为正方形；按上述类似方法，如图2，抛物线C1：y1=a1x（x﹣b1）经过变换可得到抛物线C2：y2=a2x（x﹣b2），C2与x轴的正半轴交与点A2，且其对称轴分别交抛物线C1，C2于点B2，D2，此时四边形OB2A2D2也恰为正方形；按上述类似方法，如图3，可得到抛物线C3：y3=a3x（x﹣b3）与正方形OB3A3D3．请探究以下问题：

    （1）填空：a1= ，b1= ；

    （2）求出C2与C3的解析式；

    （3）按上述类似方法，可得到抛物线Cn：yn=anx（x﹣bn）与正方形OBnAnDn（n≥1）．

    ①请用含n的代数式直接表示出Cn的解析式；

    ②当x取任意不为0的实数时，试比较y2015与y2016的函数值的大小并说明理由．

    查看答案和解析>>

    同步练习册答案