
【题目】如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm. sin75°≈0.97,cos75°≈0.26,![]() ≈1.73
≈1.73
(1)求该台灯照亮水平桌面的宽度BC.
(2)人在此台灯下看书,将其侧面抽象成如图2所示的几何图形,若书与水平桌面的夹角∠EFC为60°,书的长度EF为24cm,点P为眼睛所在位置,当点P在EF 的垂直平分线上,且到EF距离约为34cm(人的正确看书姿势是眼睛离书距离约1尺≈34cm)时,称点P为“最佳视点”.请通过计算说明最佳视点P在不在灯光照射范围内?
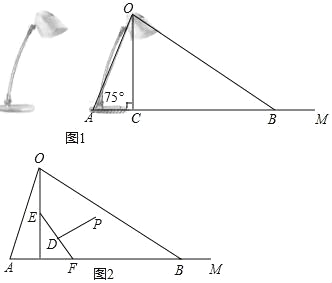
【答案】(1) 该台灯照亮水平面的宽度BC大约是83.9cm;(2) 最佳视点P在灯光照射范围内,理由见解析.
【解析】
试题分析:(1)在直角三角形ACO中,根据sin75°=![]() ,求出OC,在直角三角形BCO中,tan30°=
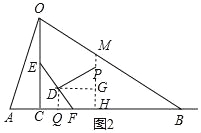
,求出OC,在直角三角形BCO中,tan30°=![]() ,求出BC即可.(2)如图,过点P作PH⊥AB于H,交OB于M,过点D作DG⊥PH于G,DQ⊥AB于Q,则四边形DGHQ为矩形,∠GDF=∠EFC=∠DPG=60°,求出PH,MH的长即可判断.
,求出BC即可.(2)如图,过点P作PH⊥AB于H,交OB于M,过点D作DG⊥PH于G,DQ⊥AB于Q,则四边形DGHQ为矩形,∠GDF=∠EFC=∠DPG=60°,求出PH,MH的长即可判断.
试题解析:(1)在直角三角形ACO中,sin75°=![]() ,
,
解得OC=50×0.97≈48.5,
在直角三角形BCO中,tan30°=![]() ,
,
解得BC=1.73×48.5≈83.9.
答:该台灯照亮水平面的宽度BC大约是83.9cm,
(2)如图,过点P作PH⊥AB于H,交OB于M,过点D作DG⊥PH于G,DQ⊥AB于Q,则四边形DGHQ为矩形,∠GDF=∠EFC=∠DPG=60°
由题意DE=DF=12,DP=34,
∴PG=17,QH=DG=17![]() ,QF=6,GH=DQ=6
,QF=6,GH=DQ=6![]() ,
,
∴PH=PH+GH=17+6![]() ≈27.38,
≈27.38,
又∵CH=6+17![]() ≈35.41
≈35.41
∴HB=CB﹣CH=83.9﹣35.41≈48.49,
∵∠OBC=30°,tan∠OBC=1:![]() ,
,
∴MH=HB÷![]() =48.49÷
=48.49÷![]() ≈28.03,
≈28.03,
∵27.38<28.03,
∴最佳视点P在灯光照射范围内.


科目:初中数学 来源: 题型:
【题目】正比例函数 y=(k-2)x 中,y 随 x 的增大而减小,则 k 的取值范围是( )
A. k≥2 B. k≤2 C. k>2 D. k<2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.表是甲班和乙班成绩最好的5名学生的比赛成绩.
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 100 | 98 | 102 | 97 | 103 | 500 |
乙班 | 99 | 100 | 95 | 109 | 97 | 500 |
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)甲班的优秀率为60%,则乙班的优秀率为 ;
(2)甲班比赛成绩的方差S甲2=![]() ,求乙班比赛成绩的方差;
,求乙班比赛成绩的方差;
(3)根据以上信息,你认为应该把团体第一名的奖状给哪一个班?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四舍五入法按要求对0.05049分别取近似值,其中错误的是( )
A、0.1(精确到0.1)B、0.05(精确到百分位)
C、0.05(精确到千分位)D、0.050(精确到0.001)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张爷爷晚饭以后外出散步,碰到老邻居,交谈了一会儿,返回途中在读报栏前看了一会儿报,如图是据此情境画出的图象,请你回答下面的问题:
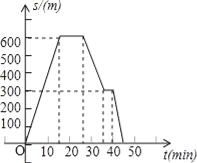
(1)张爷爷是在什么地方碰到老邻居的,交谈了多长时间?
(2)读报栏大约离家多远?
(3)图中反映了哪些变量之间的关系?其中哪个是自变量?哪个是因变量?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门. ![]()
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个计算器,计算![]() 时只能显示1.41421356237十三位(包括小数点),现在想知道7后面的数字是什么,可以在这个计算器中计算下面哪一个值( )
时只能显示1.41421356237十三位(包括小数点),现在想知道7后面的数字是什么,可以在这个计算器中计算下面哪一个值( )
A. 10![]() B. 10(
B. 10(![]() -1) C. 100
-1) C. 100![]() D.
D. ![]() -1
-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com