
【题目】已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )
A.abc<0
B.﹣3a+c<0
C.b2﹣4ac≥0
D.将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c
【答案】B
【解析】解:A.由开口向下,可得a<0;又由抛物线与y轴交于负半轴,可得c<0,然后由对称轴在y轴右侧,得到b与a异号,则可得b>0,故得abc>0,故本选项错误;
B.根据图知对称轴为直线x=2,即 ![]() =2,得b=﹣4a,再根据图象知当x=1时,y=a+b+c=a﹣4a+c=﹣3a+c<0,故本选项正确;
=2,得b=﹣4a,再根据图象知当x=1时,y=a+b+c=a﹣4a+c=﹣3a+c<0,故本选项正确;
C.由抛物线与x轴有两个交点,可得b2﹣4ac>0,故本选项错误;
D.y=ax2+bx+c= ![]() ,∵
,∵ ![]() =2,∴原式=
=2,∴原式= ![]() ,∴向左平移2个单位后所得到抛物线的解析式为
,∴向左平移2个单位后所得到抛物线的解析式为 ![]() ,故本选项错误;
,故本选项错误;
故答案为:B.
根据图像开口向下,可得a<0;又由抛物线与y轴交于负半轴,可得c<0,然后由对称轴在y轴右侧,得到b与a异号,则可得b>0,得到abc>0;由对称轴为直线x=2,得到y=a+b+c=a﹣4a+c=﹣3a+c<0,由抛物线与x轴有两个交点,可得b2﹣4ac>0.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD的两条边在坐标轴上,点D与坐标原点O重合,且AD=8,AB=6.如图2,矩形ABCD沿OB方向以每秒1个单位长度的速度运动,同时点P从A点出发也以每秒1个单位长度的速度沿矩形ABCD的边AB经过点B向点C运动,当点P到达点C时,矩形ABCD和点P同时停止运动,设点P的运动时间为t秒.
(1)当t=5时,请直接写出点D,点P的坐标;
(2)当点P在线段AB或线段BC上运动时,求出△PBD的面积S关于t的函数关系式,并写出相应t的取值范围;
(3)点P在线段AB或线段BC上运动时,作PE⊥x轴,垂足为点E,当△PEO与△BCD相似时,求出相应的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有正方形的中心都在原点,且各边也都与x轴或y轴平行,从内向外,它们的边长依次为2,4,6,8,…顶点依次用A1、A2、A3、A4表示,则顶点A2020的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是⊙
是⊙ ![]() 的直径,
的直径, ![]() 、
、 ![]() 为⊙
为⊙ ![]() 上位于
上位于 ![]() 异侧的两点,连接
异侧的两点,连接 ![]() 并延长至点
并延长至点 ![]() ,使得
,使得 ![]() ,连接
,连接 ![]() 交⊙
交⊙ ![]() 于点
于点 ![]() ,连接
,连接 ![]() 、
、 ![]() 、
、 ![]() .
.
(1)证明: ![]() ;
;
(2)若 ![]() ,求
,求 ![]() 的度数;
的度数;
(3)设 ![]() 交
交 ![]() 于点
于点 ![]() ,若
,若 ![]() 是
是 ![]() 的中点,求
的中点,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面 ![]() 与通道
与通道 ![]() 平行),通道水平宽度
平行),通道水平宽度 ![]() 为8米,
为8米, ![]() ,通道斜面
,通道斜面 ![]() 的长为6米,通道斜面
的长为6米,通道斜面 ![]() 的坡度
的坡度 ![]() .
.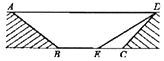
(1)求通道斜面 ![]() 的长为米;
的长为米;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面 ![]() 的坡度变缓,修改后的通道斜面
的坡度变缓,修改后的通道斜面 ![]() 的坡角为30°,求此时
的坡角为30°,求此时 ![]() 的长.(结果保留根号)
的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AF平分∠BAD交BC于E,交DC延长线于F,点G为EF的中点,连结DG.
(1)求证:BC=DF;
(2)连BD,求BD:DG的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
如图,AB和CD相交于点O,EF∥AB,∠C=∠COA,∠D=∠BOD.求证:∠A=∠F.

证明:∵∠C=∠COA,∠D=∠BOD,
又∵∠COA=∠BOD( ),
∴∠C= ( ).
∴AC∥BD( ).
∴∠A= ( ).
∵EF∥AB,
∴∠F= ( ).
∴∠A=∠F( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com