
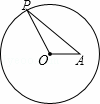
如图,半径为3的⊙O内有一点A,OA=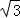 ,点P在⊙O上,当∠OPA最大时,PA的长等于( )
,点P在⊙O上,当∠OPA最大时,PA的长等于( )
A. 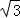 B.
B.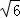 C3 D. 2
C3 D. 2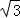
科目:初中数学 来源: 题型:
如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )
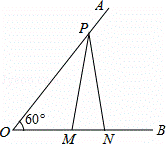
A. 3 B.4 C.5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③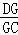 =
=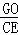 ;④(a﹣b)2•S△EFO=b2•S△DGO.其中结论正确的个数是( )
;④(a﹣b)2•S△EFO=b2•S△DGO.其中结论正确的个数是( )
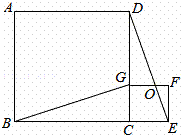
A. 4个 B.3个 C.2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知∠MON=90°,A是∠MON内部的一点,过点A作AB⊥ON,垂足为点B,AB=3厘米,OB=4厘米,动点E,F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运 动.设运动时间为t秒(t>0).
动.设运动时间为t秒(t>0).
(1)当t=1秒时,△EOF与△ABO是否相似?请说明理由;
(2)在运动过程中,不论t取何值时,总有EF⊥OA.为什么?
(3)连接AF,在运动过程中,是否存在某一时刻t,使得S△AEF=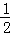 S四边形AEOF?若存在,请求出此时t的值;若不存在,请说明理由.
S四边形AEOF?若存在,请求出此时t的值;若不存在,请说明理由.
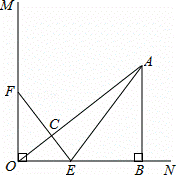
查看答案和解析>>
科目:初中数学 来源: 题型:
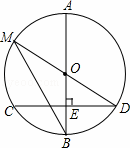
如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com