
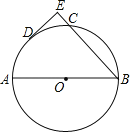
【题目】如图,AB是⊙O的直径,点C、D在半圆上,![]() ,过D作DE⊥BC于E.
,过D作DE⊥BC于E.
(1)求证:DE是⊙O的切线.
(2)若DE=2CE=4,求⊙O的半径.
【答案】(1)证明见解析;(2)5
【解析】
(1)如图,连接OD、AC,由AB是直径可得∠ACB=90°,根据DE⊥BC可得DE//AC,根据垂径定理的推论可得OD⊥AC,即可证明OD⊥DE,由点D在圆上即可证明DE是⊙O的切线;(2)作OF⊥BC于F,可得四边形OFED是矩形,可得OF=DE=4,OD=EF,由垂径定理可得BF=CF,设⊙O的半径为R,在Rt△AOF中,利用勾股定理求出R值即可.
(1)如图,连接OD、AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AC⊥BC,
∵DE⊥BC,
∴DE∥AC,
∵![]() ,
,
∴OD⊥AC,
∴DE⊥OD,
∵D在⊙O上,
∴DE是⊙O的切线;
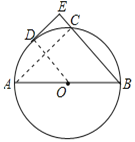
(2)如图,作OF⊥BC于F,
∴BF=CF,
∵DE⊥BE,OD⊥DE,OF⊥BC,
∴四边形OFED是矩形,
∴OF=DE=4,OD=EF,
∵DE=2CE=4,
∴CE=2,
设⊙O的半径为R,则BF=CF=R﹣2,
在Rt△BOF中,BF2+OF2=OA2,
∴(R﹣2)2+42=R2,
解得R=5,
即⊙O的半径为5.


科目:初中数学 来源: 题型:
【题目】如图(1)是一款手机支架,忽略支管的粗细,得到它的简化结构图如图(2)所示.已知支架底部支架CD平行于水平面,EF⊥OE,GF⊥EF,支架可绕点O旋转,OE=20cm,EF=20![]() cm.如图(3)若将支架上部绕O点逆时针旋转,当点G落在直线CD上时,测量得∠EOG=65°.
cm.如图(3)若将支架上部绕O点逆时针旋转,当点G落在直线CD上时,测量得∠EOG=65°.
(1)求FG的长度(结果精确到0.1);
(2)将支架由图(3)转到图(4)的位置,若此时F、O两点所在的直线恰好于CD垂直,点F的运动路线的长度称为点F的路径长,求点F的路径长.
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项答题竞猜活动,在6个式样、大小都相同的箱子中有且只有一个箱子里藏有礼物.参与选手将回答5道题目,每答对一道题,主持人就从6个箱子中去掉一个空箱子.而选手一旦答错,即取消后面的答题资格,从剩下的箱子中选取一个箱子.
(1)一个选手答对了4道题,求他选中藏有礼物的箱子的概率;
(2)已知一个选手选中藏有礼物的箱子的概率为![]() ,则他答对了几道题?
,则他答对了几道题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有一长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为( )米.
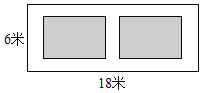
A. 2B. 1C. 8或1D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
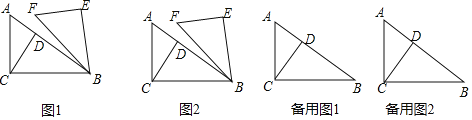
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 于点D,将
于点D,将![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() 得到
得到![]()
![]() 如图2,当
如图2,当![]() 时,求点C、E之间的距离;
时,求点C、E之间的距离;
![]() 在旋转过程中,当点A、E、F三点共线时,求AF的长;
在旋转过程中,当点A、E、F三点共线时,求AF的长;
![]() 连结AF,记AF的中点为P,请直接写出线段CP长度的最小值.
连结AF,记AF的中点为P,请直接写出线段CP长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的纸箱里有分别标有汉字“热”“爱”“祖”“国”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先摇匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“国”字的概率.
(2)小红从中任取球,不放回,再从中任取一球,请用树状图或列表法,求小红取出的两个球上的汉字恰好能组成“爱国”或“祖国”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,小正方形网格的边长为 1个单位长度,△ABC的三个顶点的坐标分别为A(﹣3,4),B(﹣5,2),C(﹣2,1).
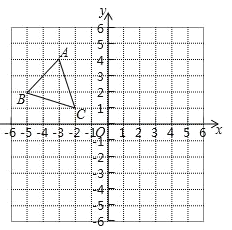
(1)画出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() 并写出点
并写出点![]() 的坐标;
的坐标;
(2)将![]() 绕点O逆时针旋转
绕点O逆时针旋转![]() ,画出旋转后的
,画出旋转后的![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问锯几何?”用现代的数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意,CD长为( )

A.12寸 B.13寸 C.24寸 D.26寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=5cm,BC=10cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时点Q从点B出发沿BC边向点C以每秒2cm的速度移动,P、Q两点在分别到达B、C两点时就停止移动,设两点移动的时间为t秒,解答下列问题:
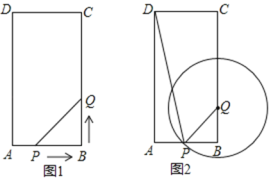
(1)如图1,当t为几秒时,△PBQ的面积等于4cm2?
(2)如图2,以Q为圆心,PQ为半径作⊙Q.在运动过程中,是否存在这样的t值,使⊙Q正好与四边形DPQC的一边(或边所在的直线)相切?若存在,求出t值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com