
【题目】已知二次函数y=a(x+1)2 (a≠0)的图象经过点A(1,8).
(1)求此二次函数的表达式;
(2)写出这个二次函数图象的顶点坐标、对称轴;
(3)试判断点B(-2,2)和C(m,2m-1)是否在此二次函数的图象上?
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】合肥市拟将徽州大道南延至庐江县庐城镇,庐江段的一段土方工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该土方工程分成两部分,甲队做完其中一部分工程用了x天,乙队做完另一部分工程用了y天,若x,y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,请用含x的式子表示y,并求出两队实际各做了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC 中,AD 是 BC 边上的中线.
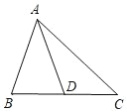
(1)画出与△ACD 关于点 D 成中心对称的三角形;
(2)找出与 AC 相等的线段;
(3)探索:△ABC 中,AB+AC 与中线 AD 之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果两条线段将一个三角形分成 3个等腰三角形,我们把这两条线段叫做这个三角形的“三分线”.例如:如图①,线段![]() 、
、![]() 把一个顶角为
把一个顶角为![]() 的等腰
的等腰![]() 分成了 3个等腰三角形,则线段
分成了 3个等腰三角形,则线段![]() 、
、![]() 就是等腰
就是等腰![]() 的“三分线”.
的“三分线”.

(1)图②是一个顶角为 45°的等腰三角形,在图中画出“三分线”,并标出每个等腰三角形顶角的度数.
(2)如图③,在![]() 边上取一点
边上取一点![]() ,令
,令![]() 可以分割出第一个等腰
可以分割出第一个等腰![]() ,接着又需要考虑如何将
,接着又需要考虑如何将![]() 分成2个等腰三角形,即可画出所需要的“三分线”,类比该方法,在图④中画出
分成2个等腰三角形,即可画出所需要的“三分线”,类比该方法,在图④中画出![]() 的“三分线”,并标出每个等腰三角形顶角的度数;
的“三分线”,并标出每个等腰三角形顶角的度数;

(3)在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
①画出![]() ;(尺规画图,不写作法,保留作图痕迹)
;(尺规画图,不写作法,保留作图痕迹)
②画出![]() 的“三分线”,并做适当的标注.
的“三分线”,并做适当的标注.

查看答案和解析>>
科目:初中数学 来源: 题型:
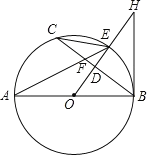
【题目】如图,AB为⊙O的直径,OD⊥弦BC于点D,交⊙O于点E,AE与BC交于点F,点H为OD延长线上一点,且∠OHB=∠AEC.
(1)求证:BH是⊙O的切线;
(2)求证:CE2=EF·EA;
(3)若⊙O的半径为5,sin∠C=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
(1)请在如图所示的网格平面内作出平面直角坐标系,使点A坐标为(1,3)点B坐标为(2,1);
(2)请作出△ABC关于y轴对称的△A'B'C',并写出点C'的坐标;
(3)判断△ABC的形状.并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
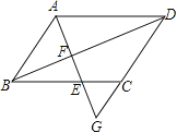
【题目】如图,在平行四边形ABCD中,点G在边DC的延长线上,AG交边BC于点E,交对角线BD于点F.
(1)求证:AF2=EFFG;
(2)如果EF=![]() ,FG=
,FG=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用3 000元购进某种干果销售,由于销售状况良好,超市又调拨9 000元购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量比第一次的2倍还多300 kg.如果超市按9元/kg的价格出售,当大部分干果售出后,余下的600 kg按售价的八折售完.
(1)该种干果第一次的进价是多少?
(2)超市销售这种干果共盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com