
【题目】如图,抛物线y=ax2+bx+c交x轴分别于点A(﹣3,0),B(1,0),交y轴正半轴于点D,抛物线顶点为C.下列结论
①2a﹣b=0;
②a+b+c=0;
③当m≠﹣1时,a﹣b>am2+bm;
④当△ABC是等腰直角三角形时,a=![]() ;
;
⑤若D(0,3),则抛物线的对称轴直线x=﹣1上的动点P与B、D两点围成的△PBD周长最小值为3![]() ,其中,正确的个数为( )
,其中,正确的个数为( )
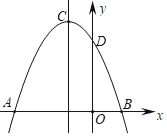
A.2个B.3个C.4个D.5个
【答案】D
【解析】
把A、B两点坐标代入抛物线的解析式并整理即可判断①②;
根据抛物线的顶点和最值即可判断③;
求出当△ABC是等腰直角三角形时点C的坐标,进而可求得此时a的值,于是可判断④;
根据利用对称性求线段和的最小值的方法(将军饮马问题)求解即可判断⑤.
解:把A(﹣3,0),B(1,0)代入y=ax2+bx+c得到![]() ,消去c得到2a﹣b=0,故①②正确;
,消去c得到2a﹣b=0,故①②正确;
∵抛物线的对称轴是直线x=﹣1,开口向下,∴x=﹣1时,y有最大值,最大值=a﹣b+c,
∵m≠﹣1,∴a﹣b+c>am2+bm+c,∴a﹣b>am2+bm,故③正确;
当△ABC是等腰直角三角形时,C(﹣1,2),
可设抛物线的解析式为y=a(x+1)2+2,把(1,0)代入解得a=﹣![]() ,故④正确,
,故④正确,
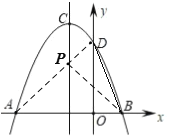
如图,连接AD交抛物线的对称轴于P,连接PB,则此时△BDP的周长最小,最小值=PD+PB+BD=PD+PA+BD=AD+BD,
∵AD=![]() =3
=3![]() ,BD=
,BD=![]() =
=![]() ,
,
∴△PBD周长最小值为3![]() ,故⑤正确.
,故⑤正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点O在AC上,以O为圆心,OC为半径作⊙O,过点A作AD⊥BO交BO的延长线于点D.则下列结论中:①点A、B、C、D在同一个圆上;②∠ABC=2∠CAD;③若∠BOC=∠BAD,则AB与⊙O相切,正确的结论是( )
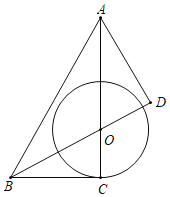
A.①②③B.①②C.②③D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y![]() (x>0)的图象经过A,B两点,若菱形ABCD的面积为2
(x>0)的图象经过A,B两点,若菱形ABCD的面积为2![]() ,则k的值为( )
,则k的值为( )
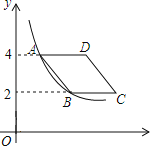
A. 2B. 3C. 4D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
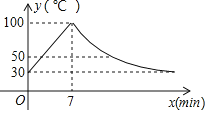
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃停止加热,水温开始下降,此时水温![]() (℃)与开机后用时
(℃)与开机后用时![]() (
(![]() )成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温
)成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温![]() (℃)与时间
(℃)与时间![]() (
(![]() )的关系如图所示:
)的关系如图所示:
(1)分别写出水温上升和下降阶段![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)怡萱同学想喝高于50℃的水,请问她最多需要等待多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
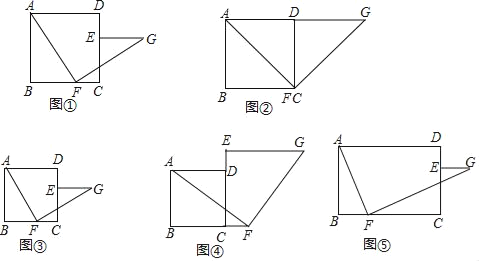
【题目】(综合与实践)如图①,在正方形ABCD中,点E、F分别在射线CD、BC上,且BF=CE,将线段FA绕点F顺时针旋转90°得到线段FG,连接EG,试探究线段EG和BF的数量关系和位置关系.
(观察与猜想)任务一:“智慧小组”首先考虑点E、F的特殊位置如图②,当点E与点D重合,点F与点C重合时,易知:EG与BF的数量关系是 ,EG与BF的位置关系是 .
(探究与证明)任务二:“博学小组”同学认为E、F不一定必须在特殊位置,他们分两种情况,一种是点E、F分别在CD、BC边上任意位置时(如图③);一种是点E、F在CD、BC边的延长线上的任意位置时(如图④),线段EG与BF的数量关系与位置关系仍然成立.请你选择其中一种情况给出证明.
(拓展与延伸)“创新小组”同学认为,若将“正方形ABCD”改为“矩形ABCD,且![]() =k(k≠1)”,点E、F分别在射线CD、BC上任意位置时,仍将线段FA绕点F顺时针旋转90°,并适当延长得到线段FG,连接EG(如图⑤),则当线段BF、CE、AF、FG满足一个条件 时,线段EG与BF的数量关系与位置关系仍然成立.(请你在横线上直接写出这个条件,无需证明)
=k(k≠1)”,点E、F分别在射线CD、BC上任意位置时,仍将线段FA绕点F顺时针旋转90°,并适当延长得到线段FG,连接EG(如图⑤),则当线段BF、CE、AF、FG满足一个条件 时,线段EG与BF的数量关系与位置关系仍然成立.(请你在横线上直接写出这个条件,无需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你利用直角坐标平面上任意两点(x1,y1)、(x2,y2)间的距离公式![]() 解答下列问题:
解答下列问题:
已知:反比例函数![]() 与正比例函数y=x的图象交于A、B两点(A在第一象限),点F1(﹣2,﹣2)、F2(2,2)在直线y=x上.设点P(x0,y0)是反比例函数
与正比例函数y=x的图象交于A、B两点(A在第一象限),点F1(﹣2,﹣2)、F2(2,2)在直线y=x上.设点P(x0,y0)是反比例函数![]() 图象上的任意一点,记点P与F1、F2两点的距离之差d=|PF1﹣PF2|.试比较线段AB的长度与d的大小,并由此归纳出双曲线的一个重要定义(用简练的语言表述).
图象上的任意一点,记点P与F1、F2两点的距离之差d=|PF1﹣PF2|.试比较线段AB的长度与d的大小,并由此归纳出双曲线的一个重要定义(用简练的语言表述).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的二次函数y=2x2+bx+c.当x=1时,y=4;当x=﹣2,y=﹣5.
(1)求y关于x的二次函数的解析式;
(2)在直角坐标系中把(1)中的图象抛物线平移到顶点与原点重合,应该怎样平移?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com