
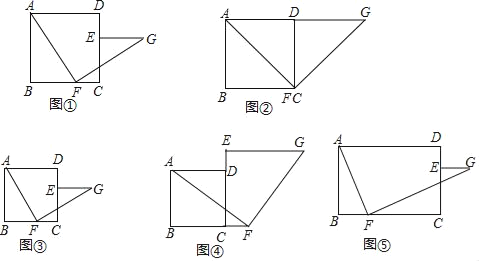
【题目】(综合与实践)如图①,在正方形ABCD中,点E、F分别在射线CD、BC上,且BF=CE,将线段FA绕点F顺时针旋转90°得到线段FG,连接EG,试探究线段EG和BF的数量关系和位置关系.
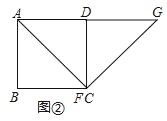
(观察与猜想)任务一:“智慧小组”首先考虑点E、F的特殊位置如图②,当点E与点D重合,点F与点C重合时,易知:EG与BF的数量关系是 ,EG与BF的位置关系是 .
(探究与证明)任务二:“博学小组”同学认为E、F不一定必须在特殊位置,他们分两种情况,一种是点E、F分别在CD、BC边上任意位置时(如图③);一种是点E、F在CD、BC边的延长线上的任意位置时(如图④),线段EG与BF的数量关系与位置关系仍然成立.请你选择其中一种情况给出证明.
(拓展与延伸)“创新小组”同学认为,若将“正方形ABCD”改为“矩形ABCD,且![]() =k(k≠1)”,点E、F分别在射线CD、BC上任意位置时,仍将线段FA绕点F顺时针旋转90°,并适当延长得到线段FG,连接EG(如图⑤),则当线段BF、CE、AF、FG满足一个条件 时,线段EG与BF的数量关系与位置关系仍然成立.(请你在横线上直接写出这个条件,无需证明)
=k(k≠1)”,点E、F分别在射线CD、BC上任意位置时,仍将线段FA绕点F顺时针旋转90°,并适当延长得到线段FG,连接EG(如图⑤),则当线段BF、CE、AF、FG满足一个条件 时,线段EG与BF的数量关系与位置关系仍然成立.(请你在横线上直接写出这个条件,无需证明)
【答案】【观察与猜想】EG=BF,EG∥BF;【探究与证明】见解析;【拓展与延伸】![]() =
=![]() =k(k≠1).
=k(k≠1).
【解析】
【观察与猜想】先根据SAS证明△ABC≌△GDC,得出AB=GD,∠GDC=∠B=90°,进而得出DG∥BC,△CDG是等腰直角三角形,再由等腰直角三角形的性质得出DG=CD=BC,即可得出结论;
【探究与证明】当点E、F分别在CD、BC边上任意位置时,作GM⊥BC,交BC延长线于M,先根据AAS证明△ABF≌△FMG,得出AB=FM,BF=MG,进而可得BF=CM,而BF=CE,可得MG=CE,于是四边形CEGM是矩形,继而有EG=CM,EG∥CM,即可得出结论;当点E、F在CD、BC边的延长线上的任意位置时,同上面的分析;
【拓展与延伸】作GM⊥BC,交BC延长线于M,先证明△ABF∽△FMG,得出![]() ,结合已知可得出
,结合已知可得出![]() ,
,![]() ,进而证出FM=BC,GM=CE,于是BF=CM,然后证明四边形CEGM是矩形,进而得EG=CM,EG∥CM,即可得出结论.
,进而证出FM=BC,GM=CE,于是BF=CM,然后证明四边形CEGM是矩形,进而得EG=CM,EG∥CM,即可得出结论.
【观察与猜想】EG=BF,EG∥BF;
证明:如图②,∵四边形ABCD是正方形,
∴∠B=∠BCD=∠ADC=90°,AB=BC=CD=AD,∠ACB=∠ACD=45°,
由旋转的性质得:GC=AC,∠ACG=90°,
∴∠ACB=∠GCD=45°,
∴△ABC≌△GDC(SAS),
∴AB=GD,∠GDC=∠B=90°,
∴DG∥BC,△CDG是等腰直角三角形,
∴DG=CD=BC,
∵点E与点D重合,点F与点C重合,
∴EG=BF,EG∥BF;
故答案为:EG=BF,EG∥BF;
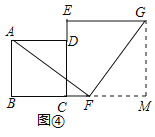
【探究与证明】证明:当点E、F分别在CD、BC边上任意位置时,如图③所示:
作GM⊥BC,交BC延长线于M,则∠GMF=90°,MG∥DC,
∵四边形ABCD是正方形,∴AB=BC,∠BCD=∠B=90°,
∴∠BAF+∠BFA=90°,
由旋转的性质得:GF=AF,∠AFG=90°,
∴∠BFA+∠MFG=90°,∴∠BAF=∠MFG,
∴△ABF≌△FMG(AAS),
∴AB=FM,BF=MG,
∵AB=BC,∴BF=CM,
∵BF=CE,∴MG=CE,
∵MG∥CE,∴四边形CEGM是平行四边形,
又∵∠M=90°,∴四边形CEGM是矩形,
∴EG=CM,EG∥CM,
∴EG=BF,EG∥BF;

当点E、F在CD、BC边的延长线上的任意位置时,如图④所示:
作GM⊥BC,交BC延长线于M,则∠M=90°,MG∥DC,
∵四边形ABCD是正方形,∴AB=BC,∠BCD=∠B=90°,
∴∠BAF+∠BFA=90°,
由旋转的性质得:GF=AF,∠AFG=90°,
∴∠BFA+∠MFG=90°,∴∠BAF=∠MFG,
∴△ABF≌△FMG(AAS),
∴AB=FM,BF=MG,
∵AB=BC,∴BF=CM,
∵BF=CE,∴MG=CE,
∵MG∥CE,∴四边形CEGM是平行四边形,
又∵∠M=90°,∴四边形CEGM是矩形,
∴EG=CM,EG∥CM,
∴EG=BF,EG∥BF;
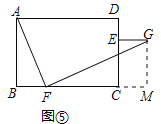
【拓展与延伸】解:![]() =k(k≠1)时,线段EG与BF的数量关系与位置关系仍然成立;理由如下:
=k(k≠1)时,线段EG与BF的数量关系与位置关系仍然成立;理由如下:
作GM⊥BC,交BC延长线于M,如图⑤所示:则∠M=90°,MG∥DC,
∵四边形ABCD是矩形,∴∠BCD=∠B=90°,
∴∠BAF+∠BFA=90°,∠B=∠M,
由旋转的性质得:∠AFG=90°,∴∠BFA+∠MFG=90°,
∴∠BAF=∠MFG,∴△ABF∽△FMG,
∴![]() ,
,
∵![]() =k,∴
=k,∴![]() =k,
=k,![]() =k,
=k,
∴FM=BC,GM=CE,∴BF=CM,
∵MG∥CE,∴四边形CEGM是平行四边形,
又∵∠M=90°,∴四边形CEGM是矩形,
∴EG=CM,EG∥CM,
∴EG=BF,EG∥BF;
故答案为:![]() =k(k≠1).
=k(k≠1).


科目:初中数学 来源: 题型:
【题目】如图所示是二次函数![]() 图象的一部分,图象过点
图象的一部分,图象过点![]() ,二次函数图象对称轴为直线
,二次函数图象对称轴为直线![]() ,给出五个结论:①
,给出五个结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 的增大而增大;④方程
的增大而增大;④方程![]() 的根为
的根为![]() ,
,![]() ;⑤
;⑤![]() 其中正确结论是( )
其中正确结论是( )

A. ①②③ B. ①③④ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块斜边长相等的等腰直角三角板按如图①摆放,斜边AB分别交CD,CE于M,N点.
(1)如果把图①中的△BCN绕点C逆时针旋转90°得到△ACF,连接FM,如图②,求证:△CMF≌△CMN;
(2)将△CED绕点C旋转,则:
①当点M,N在AB上(不与点A,B重合)时,线段AM,MN,NB之间有一个不变的关系式,请你写出这个关系式,并说明理由;
②当点M在AB上,点N在AB的延长线上(如图③)时,①中的关系式是否仍然成立?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,其中点
两点,其中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
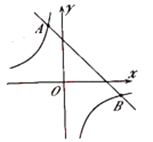
(1)根据图象,直接写出满足![]() 的
的![]() 的取值范围;
的取值范围;
(2)求这两个函数的表达式;
(3)点![]() 在线段
在线段![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
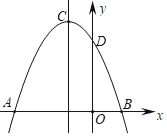
【题目】如图,抛物线y=ax2+bx+c交x轴分别于点A(﹣3,0),B(1,0),交y轴正半轴于点D,抛物线顶点为C.下列结论
①2a﹣b=0;
②a+b+c=0;
③当m≠﹣1时,a﹣b>am2+bm;
④当△ABC是等腰直角三角形时,a=![]() ;
;
⑤若D(0,3),则抛物线的对称轴直线x=﹣1上的动点P与B、D两点围成的△PBD周长最小值为3![]() ,其中,正确的个数为( )
,其中,正确的个数为( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个二次函数满足以下条件:
①函数图象与x轴的交点坐标分别为A(1,0),B(x2,y2)(点B在点A的右侧);
②对称轴是x=3;
③该函数有最小值是﹣2.
(1)请根据以上信息求出二次函数表达式;
(2)将该函数图象x>x2的部分图象向下翻折与原图象未翻折的部分组成图象“G”,平行于x轴的直线与图象“G”相交于点C(x3,y3)、D(x4,y4)、E(x5,y5)(x3<x4<x5),结合画出的函数图象求x3+x4+x5的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
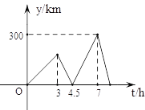
【题目】在一条笔直的公路上有A、B两地,甲、乙两辆货车都要从A地送货到B地,甲车先从A地出发匀速行驶,3小时后,乙车从A地出发,并沿同一路线匀速行驶,当乙车到达B地后立刻按原速返回,在返回途中第二次与甲车相遇。甲车出发的时间记为t (小时),两车之间的距离记为y(千米),y与t的函数关系如图所示,则乙车第二次与甲车相遇时,甲车距离A地___千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
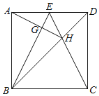
【题目】如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的是( )
A.①③B.①②③④C.①②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙![]() 与菱形
与菱形![]() 在平面直角坐标系中,点
在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 在点
在点![]() 的右侧.
的右侧.


(![]() )求菱形
)求菱形![]() 的周长.
的周长.
(![]() )若⊙
)若⊙![]() 沿
沿![]() 轴向右以每秒
轴向右以每秒![]() 个单位长度的速度平移,菱形
个单位长度的速度平移,菱形![]() 沿
沿![]() 轴向左以每秒
轴向左以每秒![]() 个单位长度的速度平移,设菱形移动的时间为(
个单位长度的速度平移,设菱形移动的时间为(![]() 秒),当⊙
秒),当⊙![]() 与
与![]() 相切,且切点为
相切,且切点为![]() 的中点时,连接
的中点时,连接![]() ,求
,求![]() 的值及
的值及![]() 的度数.
的度数.
(![]() )在(
)在(![]() )的条件下,当点
)的条件下,当点![]() 与
与![]() 所在的直线的距离为
所在的直线的距离为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com