
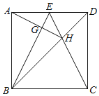
【题目】如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的是( )
A.①③B.①②③④C.①②③D.①③④
【答案】B
【解析】
根据正方形的性质证得△BAE≌△CDE,推出∠ABE=∠DCE,可知①正确;利用正方形性质证△ADH≌△CDH,求得∠HAD=∠HCD,推出∠ABE=∠HAD;求出∠ABE+∠BAG=90°;最后在△AGE中根据三角形的内角和是180°求得∠AGE=90°即可得到②正确.根据AD∥BC,求出S△BDE=S△CDE,推出S△BDES△DEH=S△CDES△DEH,即:S△BHE=S△CHD,故③正确;由∠AHD=∠CHD,得到邻补角和对顶角相等得到∠AHB=∠EHD,故④正确;
解:∵四边形ABCD是正方形,E是AD边上的中点,
∴AE=DE,AB=CD,∠BAD=∠CDA=90°,
∴△BAE≌△CDE(SAS),
∴∠ABE=∠DCE,
故①正确;
∵四边形ABCD是正方形,
∴AD=DC,∠ADB=∠CDB=45°,DH=DH,
∴△ADH≌△CDH(SAS),
∴∠HAD=∠HCD,
∵∠ABE=∠DCE
∴∠ABE=∠HAD,
∵∠BAD=∠BAH+∠DAH=90°,
∴∠ABE+∠BAH=90°,
∴∠AGB=180°90°=90°,
∴AG⊥BE,
故②正确;
∵AD∥BC,
∴S△BDE=S△CDE,
∴S△BDES△DEH=S△CDES△DEH,
即:S△BHE=S△CHD,
故③正确;
∵△ADH≌△CDH,
∴∠AHD=∠CHD,
∴∠AHB=∠CHB,
∵∠BHC=∠DHE,
∴∠AHB=∠EHD,
故④正确;
故选:B.


科目:初中数学 来源: 题型:
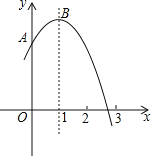
【题目】如图,抛物线![]() (m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.①抛物线
(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.①抛物线![]() 与直线
与直线![]() 有且只有一个交点;②若点
有且只有一个交点;②若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为
;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为![]() ;④点A关于直线
;④点A关于直线![]() 的对称点为C,点D、E分别在x轴和y轴上,当
的对称点为C,点D、E分别在x轴和y轴上,当![]() 时,四边形BCDE周长的最小值为
时,四边形BCDE周长的最小值为![]() .其中正确判断的序号是__
.其中正确判断的序号是__
查看答案和解析>>
科目:初中数学 来源: 题型:
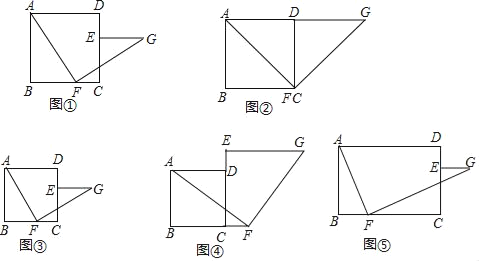
【题目】(综合与实践)如图①,在正方形ABCD中,点E、F分别在射线CD、BC上,且BF=CE,将线段FA绕点F顺时针旋转90°得到线段FG,连接EG,试探究线段EG和BF的数量关系和位置关系.
(观察与猜想)任务一:“智慧小组”首先考虑点E、F的特殊位置如图②,当点E与点D重合,点F与点C重合时,易知:EG与BF的数量关系是 ,EG与BF的位置关系是 .
(探究与证明)任务二:“博学小组”同学认为E、F不一定必须在特殊位置,他们分两种情况,一种是点E、F分别在CD、BC边上任意位置时(如图③);一种是点E、F在CD、BC边的延长线上的任意位置时(如图④),线段EG与BF的数量关系与位置关系仍然成立.请你选择其中一种情况给出证明.
(拓展与延伸)“创新小组”同学认为,若将“正方形ABCD”改为“矩形ABCD,且![]() =k(k≠1)”,点E、F分别在射线CD、BC上任意位置时,仍将线段FA绕点F顺时针旋转90°,并适当延长得到线段FG,连接EG(如图⑤),则当线段BF、CE、AF、FG满足一个条件 时,线段EG与BF的数量关系与位置关系仍然成立.(请你在横线上直接写出这个条件,无需证明)
=k(k≠1)”,点E、F分别在射线CD、BC上任意位置时,仍将线段FA绕点F顺时针旋转90°,并适当延长得到线段FG,连接EG(如图⑤),则当线段BF、CE、AF、FG满足一个条件 时,线段EG与BF的数量关系与位置关系仍然成立.(请你在横线上直接写出这个条件,无需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个四位数n,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称n为“极数”。
(1)请任意写出三个“极数”;并猜想任意一个“极数”是否是99的倍数,请说明理由;
(2)如果一个正整数a是另一个正整数b的平方,则称正整数a是完全平方数。若四位数m为“极数”,记D(m)=![]() ,求满足D(m)是完全平方数的所有m.
,求满足D(m)是完全平方数的所有m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程
(1)x2+1=3x
(2)(x﹣2)(x﹣3)=12
(3)(2x﹣3)2+x(2x﹣3)=0(因式分解法)
(4)2x2﹣4x﹣1=0(用配方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】施秉县城关镇为打造“绿色小镇”,投入资金进行河道治污.已知2017年投入资金1000万元,2019年投入资金1210万元.
(1)求该镇投入资金从2017年至2019年的年平均增长率;
(2)若2020年投入资金保持前两年的年平均增长率不变,求该镇2020年预计投入资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若实数a,b满足a+b=1时,就称点P(a,b)为“平衡点”.
(1)判断点A(3,﹣4)、B(![]() -1,2-
-1,2-![]() )是不是平衡点;
)是不是平衡点;
(2)已知抛物线y=![]() x2+(p﹣t﹣1)x+q+t﹣3(t>3)上有且只有一个“平衡点”,且当﹣2≤p≤3时,q的最小值为t,求t的值.
x2+(p﹣t﹣1)x+q+t﹣3(t>3)上有且只有一个“平衡点”,且当﹣2≤p≤3时,q的最小值为t,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
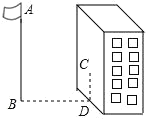
【题目】如图,在某一时刻测得1米长的竹竿竖直放置时影长1.2米,在同一时刻旗杆AB的影长不全落在水平地面上,有一部分落在楼房的墙上,他测得落在地面上影长为BD=9.6米,留在墙上的影长CD=2米,则旗杆的高度( )
A.9米B.9.6米C.10米D.10.2米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com