【题目】如图，在某一时刻测得1米长的竹竿竖直放置时影长1.2米，在同一时刻旗杆AB的影长不全落在水平地面上，有一部分落在楼房的墙上，他测得落在地面上影长为BD＝9.6米，留在墙上的影长CD＝2米，则旗杆的高度（ ）
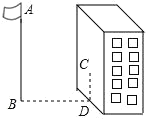
A.9米B.9.6米C.10米D.10.2米
名师指导期末冲刺卷系列答案科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，点E是AD边的中点，BD，CE交于点H，BE、AH交于点G，则下列结论：①∠ABE＝∠DCE；②AG⊥BE；③S△BHE＝S△CHD；④∠AHB＝∠EHD．其中正确的是（ ）
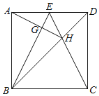
A.①③B.①②③④C.①②③D.①③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊙
与菱形
在平面直角坐标系中，点
的坐标为
点
的坐标为
，点
的坐标为
，点
在
轴上，且点
在点
的右侧．
（
）求菱形
的周长．
（
）若⊙
沿
轴向右以每秒
个单位长度的速度平移，菱形
沿
轴向左以每秒
个单位长度的速度平移，设菱形移动的时间为（
秒），当⊙
与
相切，且切点为
的中点时，连接
，求
的值及
的度数．
（
）在（
）的条件下，当点
与
所在的直线的距离为
时，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC内接于⊙O，∠B＝60°，CD是⊙O的直径，点P是CD延长线上的一点，且AP＝AC．
（1）求证：PA是⊙O的切线；
（2）若OH⊥AC，OH＝1，求DH的长．
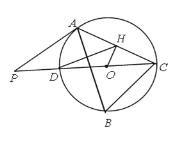
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线经过A（﹣1，0），B（5，0），C（0，
）三点．
（1）求抛物线的解析式；
（2）在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；
（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明家客厅里装有一种三位单极开关，分别控制着A（楼梯）、B（客厅）、C（走廊）三盏电灯，按下任意一个开关均可打开对应的一盏电灯，因刚搬进新房不久，不熟悉情况．
（1）若小明任意按下一个开关，则下列说法正确的是 ．
A．小明打开的一定是楼梯灯
B．小明打开的可能是卧室灯
C．小明打开的不可能是客厅灯
D．小明打开走廊灯的概率是
（2）若任意按下一个开关后，再按下另两个开关中的一个，则正好客厅灯和走廊灯同时亮的概率是多少？请用树状图法或列表法加以说明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，△ABC与△CDE是等腰直角三角形，直角边AC、CD在同一条直线上，点M、N分别是斜边AB、DE的中点，点P为AD的中点，连接AE、BD．
（1）猜想PM与PN的数量关系及位置关系，请直接写出结论；
（2）现将图①中的△CDE绕着点C顺时针旋转α（0°＜α＜90°），得到图②，AE与MP、BD分别交于点G、H．请判断（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由；
（3）若图②中的等腰直角三角形变成直角三角形，使BC=kAC，CD=kCE，如图③，写出PM与PN的数量关系，并加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB＝90°，⊙O是△ABC的内切圆，三个切点分别为D、E、F，若BF＝2，AF＝3，则△ABC的面积是
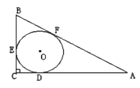
A.6B.7C.
D.12
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ABC=2∠C，AP和BQ分别为∠BAC和∠ABC的角平分线，若△ABQ的周长为18，BP=4，则AB的长为_____________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
